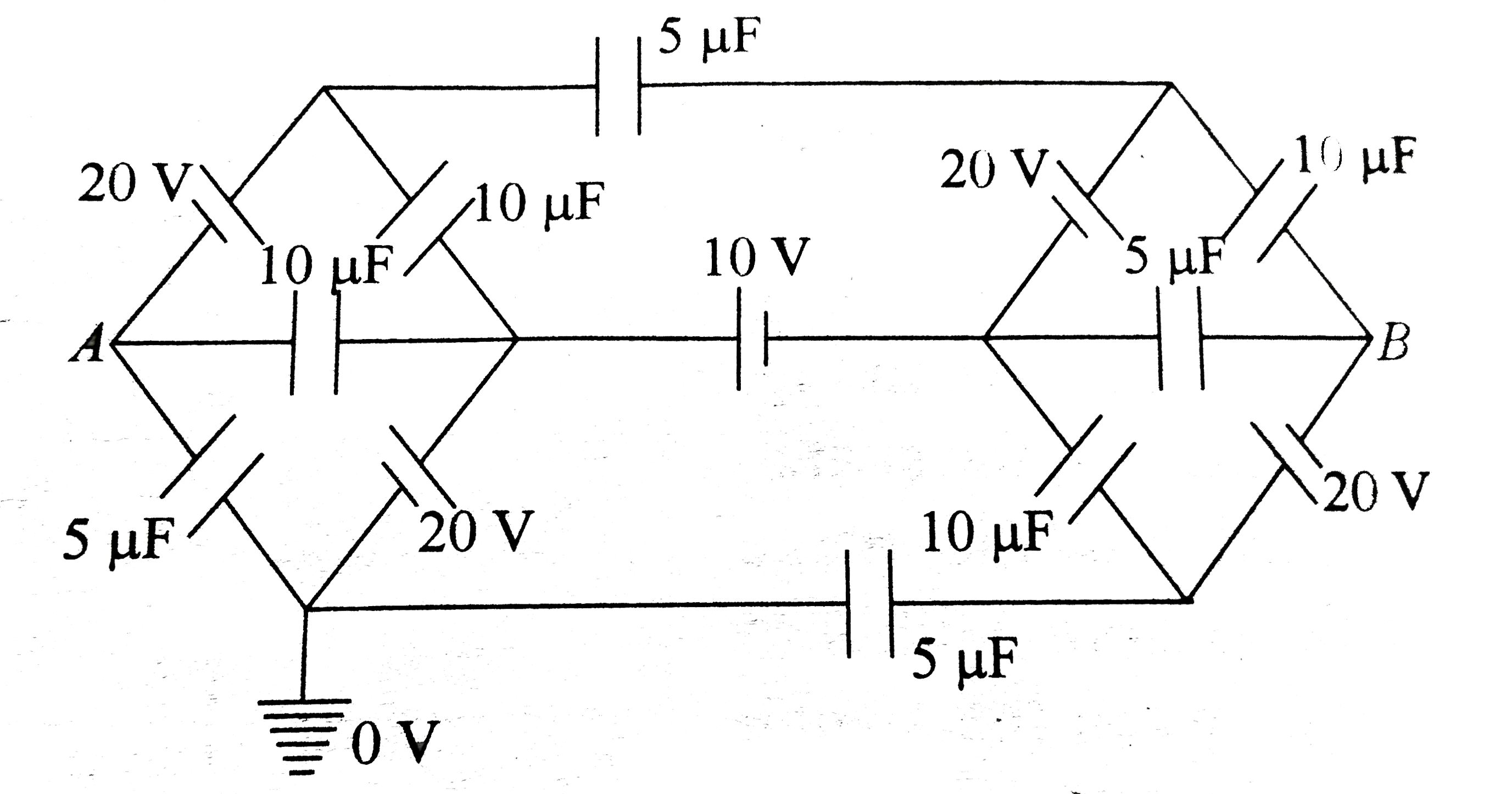
Consider the connections shown in (a) Find the capacitance between the points A and B. (b) find the charge on the three capacitors. (c ) Taking the potential at the point B to be zero, find the potential at the point D.

The <br>12 muF<br> and <br>6 muF<br> capacitors are joined in series. The equivalent of these two will have a capacitance given by <br>(1)/(C ) = (1)/(12 mu F) + (1)/(6 mu F)<br>, or, <br>C = 4 muF<br>. The combination of these two capacitors is joined in parallel with the <br>2mu F<br> capacitor. Thus, the equivalent capacitance between A and B is <br>4muF + 2muF = 6 muF<br>. (b) The charge supplied by the battery is <br>Q = CV =6muF X24V = 144muC<br>. The potential difference across the <br>2muF<br> capacitor is 24V . The charge on this capacitor is, therefore, <br>2muFX24V = 48muC<br>. The charge on the <br>12muF<br> and <br>6muF<br> capacitor is, therefore, <br>144muc - 48mu C= 96muC<br>. (c ) The potential difference across the <br>6 muF <br> capacitor is (96 muC)/(6 muF) = 16V<br>. As the potential at the point B is taken to be zero, the potential at the point D is 16 V.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Find equivalent capacitance between points A and B

View SolutionFind equivalent capacitance between points A and B,

View SolutionFind the capacitance between the point A and B of the given assemblies.

View SolutionFind the equivalent capacitance between point A and B .
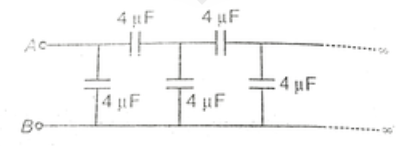
View SolutionFind the equicalent capacitance between points AandB as show in
 .
.
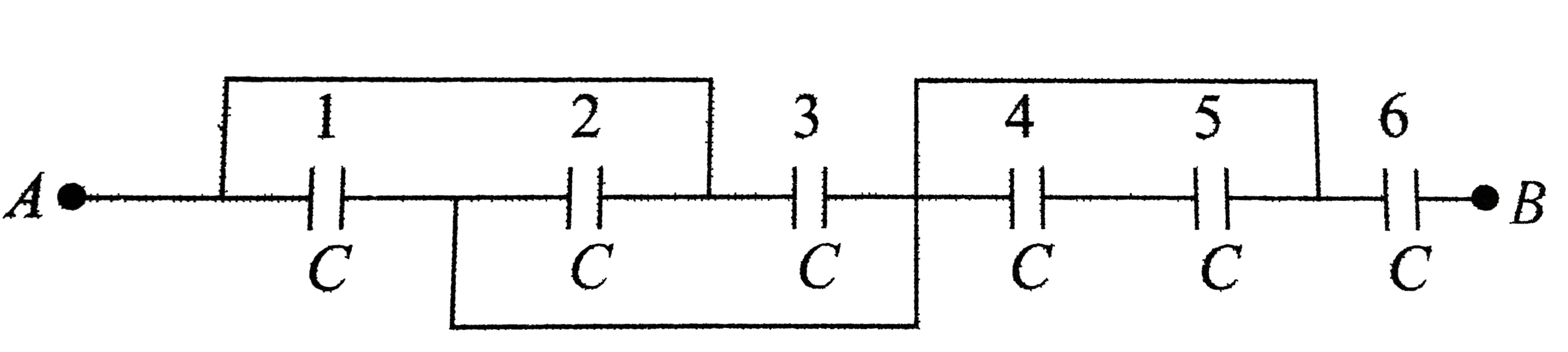
View SolutionFind equivalent capacitance between points A and B shown in figure

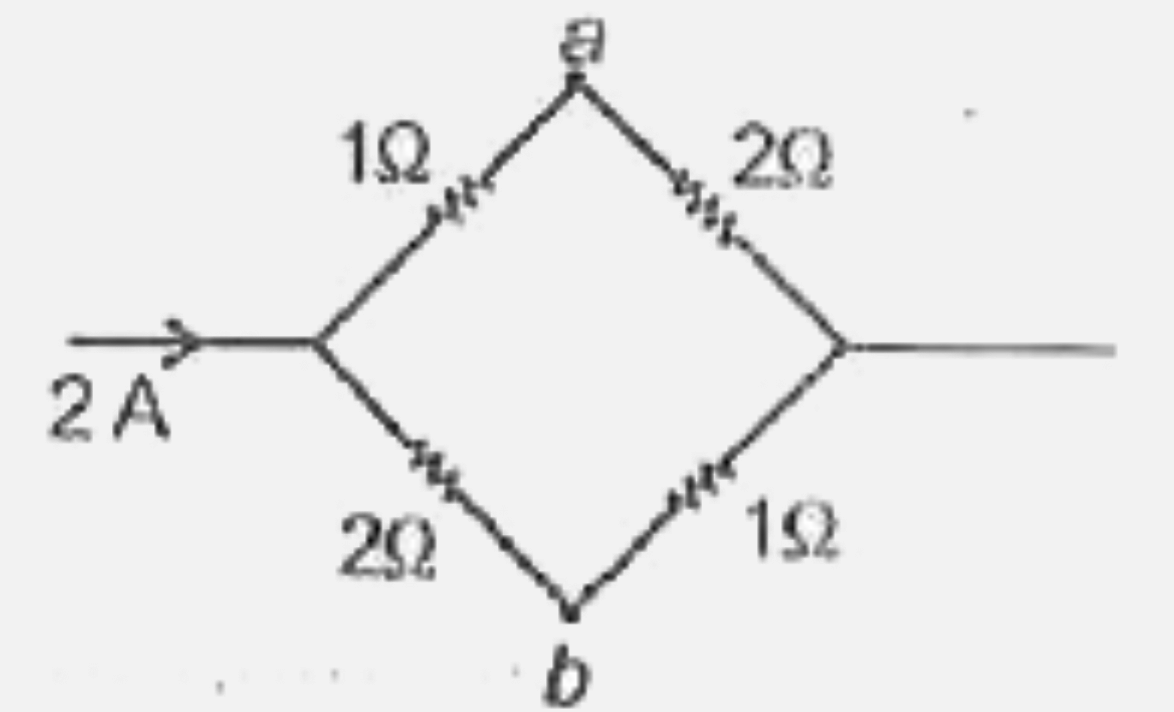
View SolutionFind theh potential difference between points a and b.
View SolutionFigure shows two capacitors of capacitance 2μF and 4μF and a cell of 90 V. The switch 'k' is such that when it is in position 1, the circuit ABCD is closed and when it is in position 2, the circuit BCEF is closed.the resistance of both the circuits is negligible os that the capacitor gets fully charged instantly. Initially the switch is in position1. then it is turned in position 2 and then in position 1. Now two cycles are completed. Find the charge (inμC) after two cycles.
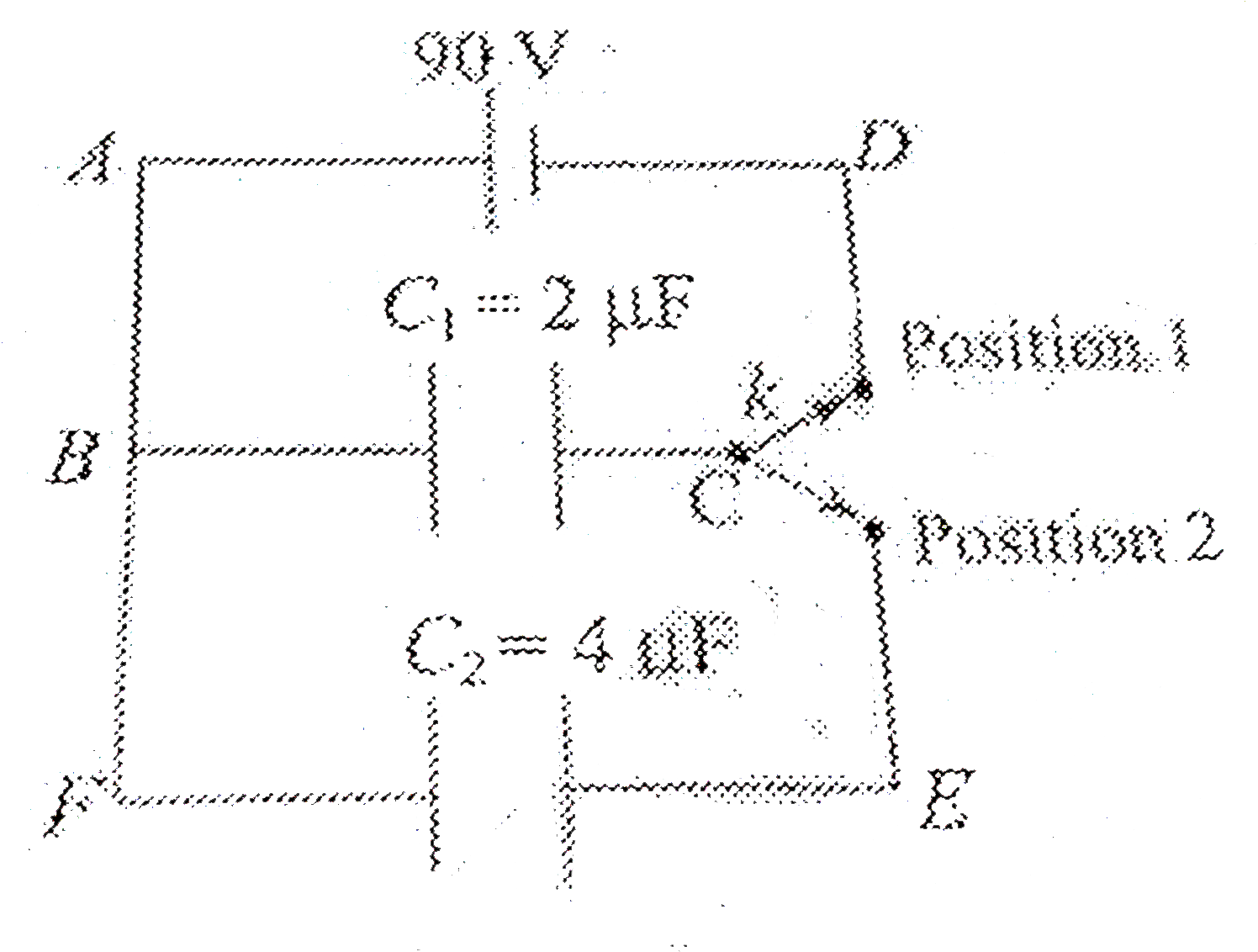
View SolutionFind the potential difference between the points A and B in the circuit shoun in.
 .
.
View SolutionThe effective capacitances between points A and B is (the capacitance of each of the capacitors is C)
View Solution
