Consider the connections shown in (a) Find the capacitance between the points A and B. (b) find the charge on the three capacitors. (c ) Taking the potential at the point B to be zero, find the potential at the point D.

, & 96 micro coulomb
, 48 micro coulomb & 96 micro coulomb ,
, 48 micro coulomb & 96 micro coulomb,
48 micro coulomb & 96 micro coulomb,
The correct Answer is:B
The 12 muF and 6 muF capacitors are joined in series. The equivalent of these two will have a capacitance given by (1)/(C ) = (1)/(12 mu F) + (1)/(6 mu F), or, C = 4 muF. The combination of these two capacitors is joined in parallel with the 2mu F capacitor. Thus, the equivalent capacitance between A and B is 4muF + 2muF = 6 muF. (b) The charge supplied by the battery is Q = CV =6muF X24V = 144muC. The potential difference across the 2muF capacitor is 24V . The charge on this capacitor is, therefore, 2muFX24V = 48muC. The charge on the 12muF and 6muF capacitor is, therefore, 144muc - 48mu C= 96muC. (c ) The potential difference across the 6 muF capacitor is (96 muC)/(6 muF) = 16V. As the potential at the point B is taken to be zero, the potential at the point D is 16 V.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer
7 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Exercise
2 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises
46 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
Similar Questions
Find equivalent capacitance between points A and B
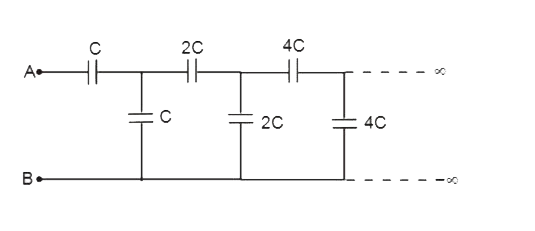
View SolutionFind equivalent capacitance between points A and B.
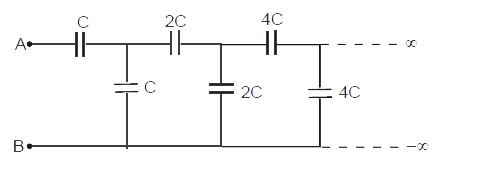
View Solution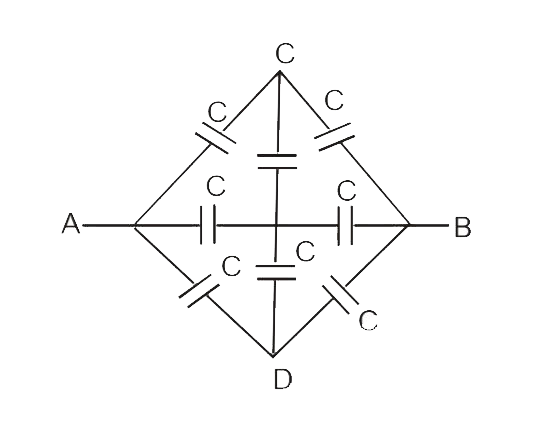 Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View Solution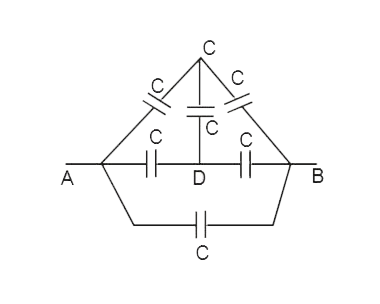 Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View SolutionFind equivalent capacitance between point A and B.
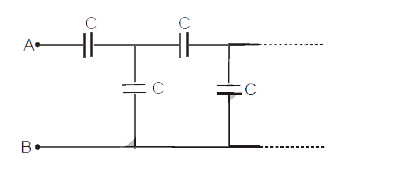
View Solution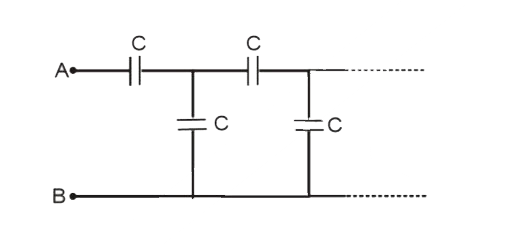 Find equivalent capacitance between point A and B
Find equivalent capacitance between point A and B
View SolutionFind equivalent capacitance between points A and B,
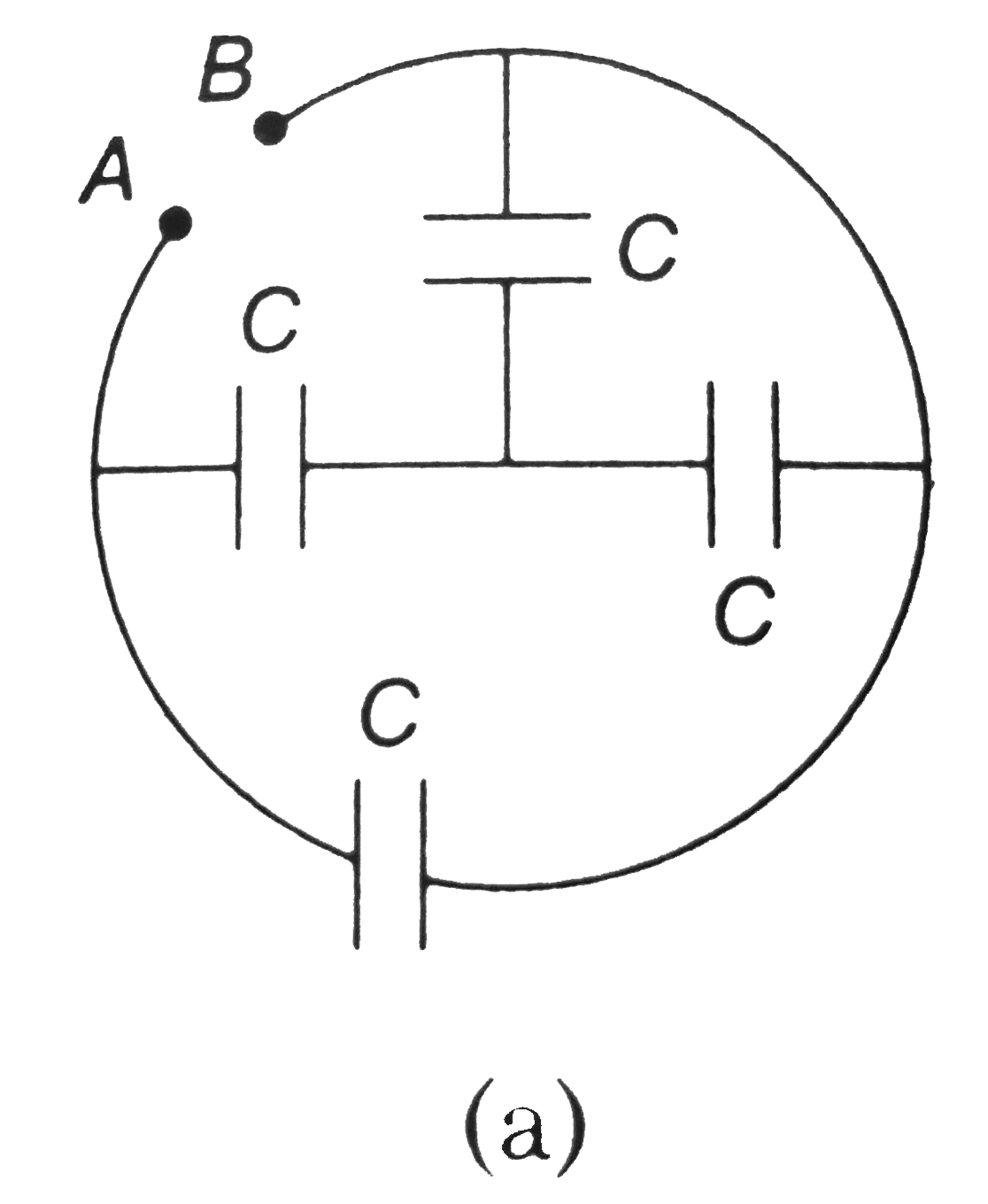
View SolutionFind the capacitance between the point A and B of the given assemblies.

View Solution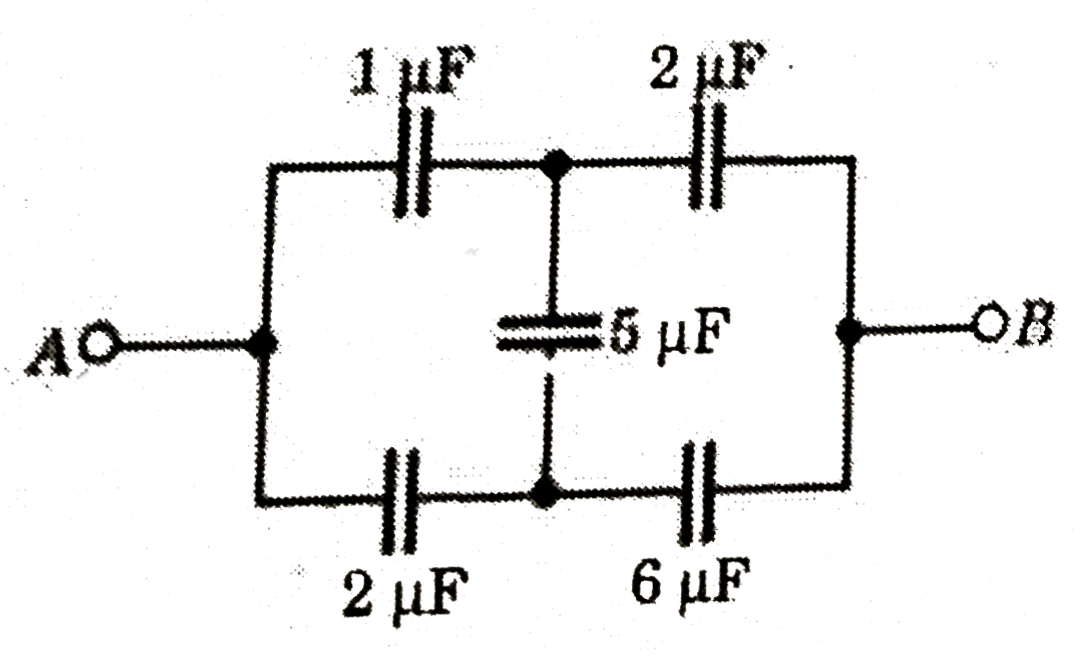
find the capacitance between the points A and B of the assembly shown in figure.
View SolutionFind the equivalent capacitance between the point A and B in figure .

View Solution
