Consider the rotation of a rod of mass m and length I from position AB to AB'. Which of the following statements are correct?

Weight of the rod is lowered by l/2
Loss of gravitational potential energy is 1/2mgl
Angular velocity is √3g/l
Rotational kinetic eneryg is ml2ω26
The correct Answer is:A, B, C, D
Equating loss of gravitational potential energy with the gain of rotational kinetic energy, we get
12Iω2=12mgl
12×ml23×ω=12mgl
ω=√3gl
Rotational kinetic energy =12ml23ω2=ml2ω26
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
If the matrix A and B are 3×3and(I−AB) is invertible, then which of the following statement is/are correct
View SolutionConsider the following statements :
1. Let ABCD be a parallelogram which is not a rectangle.
Then (AB2+BC2)≠AC2+BD2
2. If ABCD is a rhombus with AB = 4 cm, then AC2+BD2=n2 for some positive integer n.
Which of the above statements is/are correct?
View Solution
Knowledge Check
A cyclic process is shown in the figure. For the process AB which of the following statement is correct ?
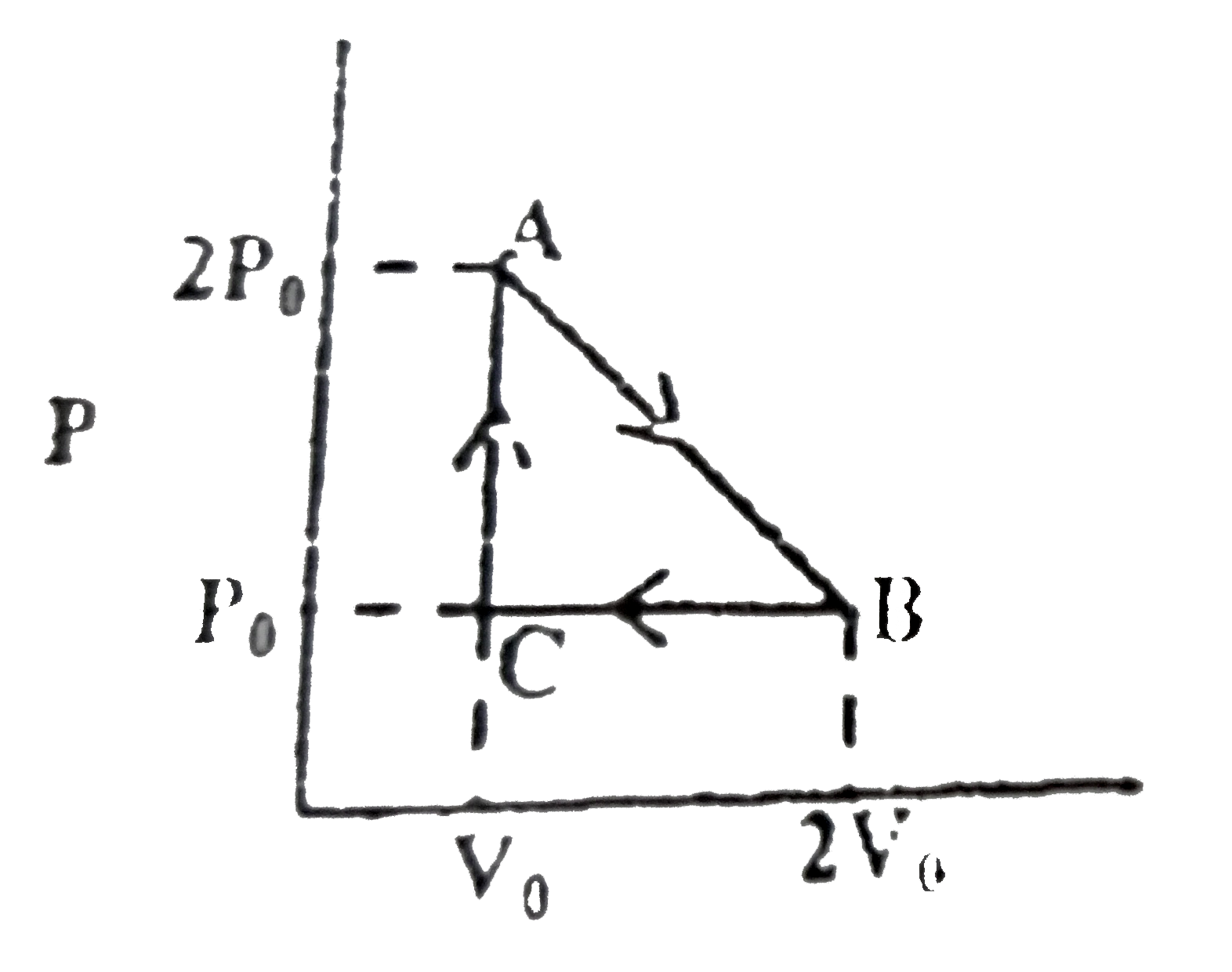 AHeat given to the system will be always −ve throughout the processBHeat given to the system will be always +ve throughout the processCFirst the heat given is +ve then −veDFirst the heat given is −ve then +ve
AHeat given to the system will be always −ve throughout the processBHeat given to the system will be always +ve throughout the processCFirst the heat given is +ve then −veDFirst the heat given is −ve then +veA thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?
 Athe angular speed of the rod after opening the hinge will remain ω0Bthe angular speed of the rod after opening the hinge will be less then ω0Cin the process of opening the hinge the kinetic energy of rod will remain conserved.Dangular momentum of rod will remain conserved about centre of mass of rod in the process of opening the hinge
Athe angular speed of the rod after opening the hinge will remain ω0Bthe angular speed of the rod after opening the hinge will be less then ω0Cin the process of opening the hinge the kinetic energy of rod will remain conserved.Dangular momentum of rod will remain conserved about centre of mass of rod in the process of opening the hingeIf the matrix A and B are of 3×3 and (I−AB) is invertible, then which of the following statement is/are correct ?
AI−BA is not invertibleBI−BA is invertibleCI−BA has for its inverse I+B(I−AB)−1ADI−BA has for its inverse I+A(I−BA)−1B
If, A and B be two matrices such that AB = A and BA=B. Then. Which of the following statements are correct ?
1. A2=A
2. B2=B
3. (AB)2=AB
View SolutionConsider the following statements
I. In India, the largest concentration of rods is found in the northern plains
II. The ratio of surfaced road to the total road length is lower in the northern plains
Which of the statements given above is are correct?
View SolutionA rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
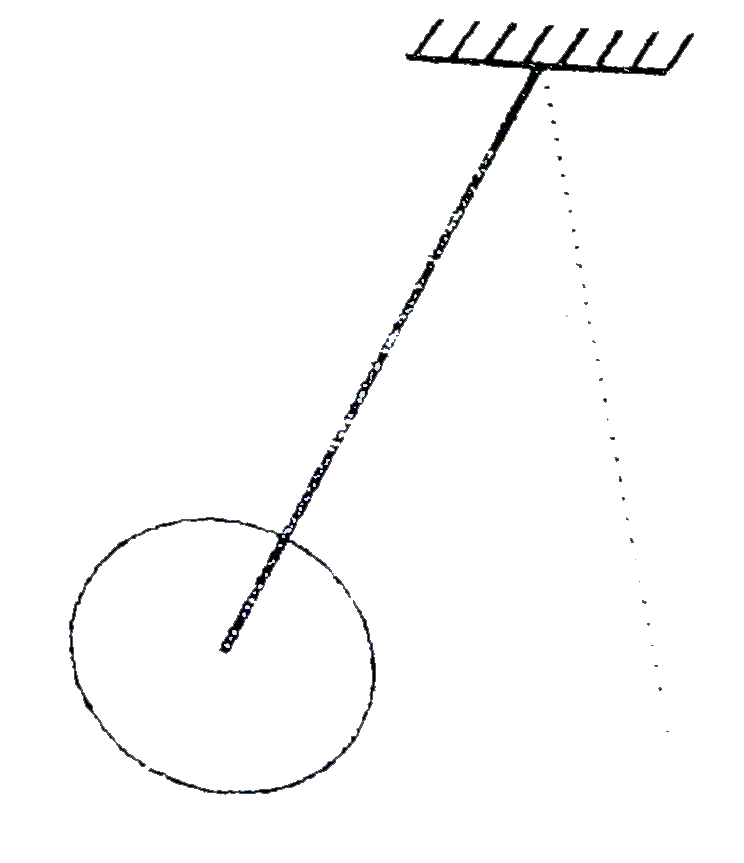
View Solution
