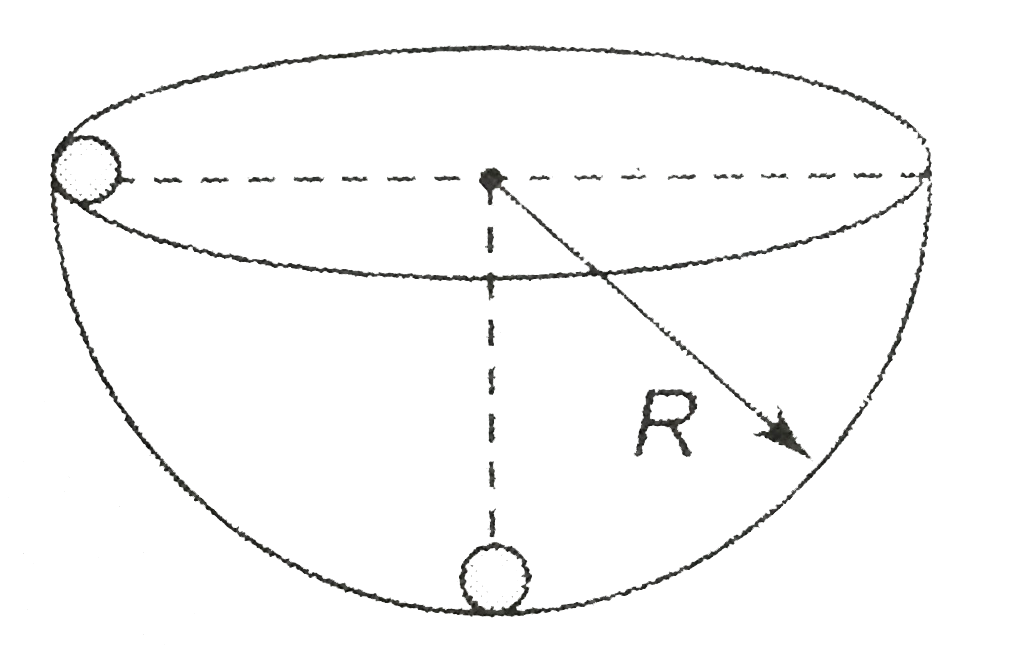
Consider the situation as shown in the figure. A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. Find the normal contact force between the solid sphere and the cup at the bottom most point.
The correct Answer is:A
Total normal force =mg+mv2R−r
Ag∈,mg(R−r)=12Iω2+12mv2

mg(R−r)=12x25mv2+12mv2
rarr 7/10mv^2=mg(R-r)<br>rarr v^2=10/7g(R-r)Therefore,→tal∥a∥lforce<br>=mg(m(10/7)g(R-r))/(R-r)<br>=mg+mg(10/7)<br>-(17/7)mg
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
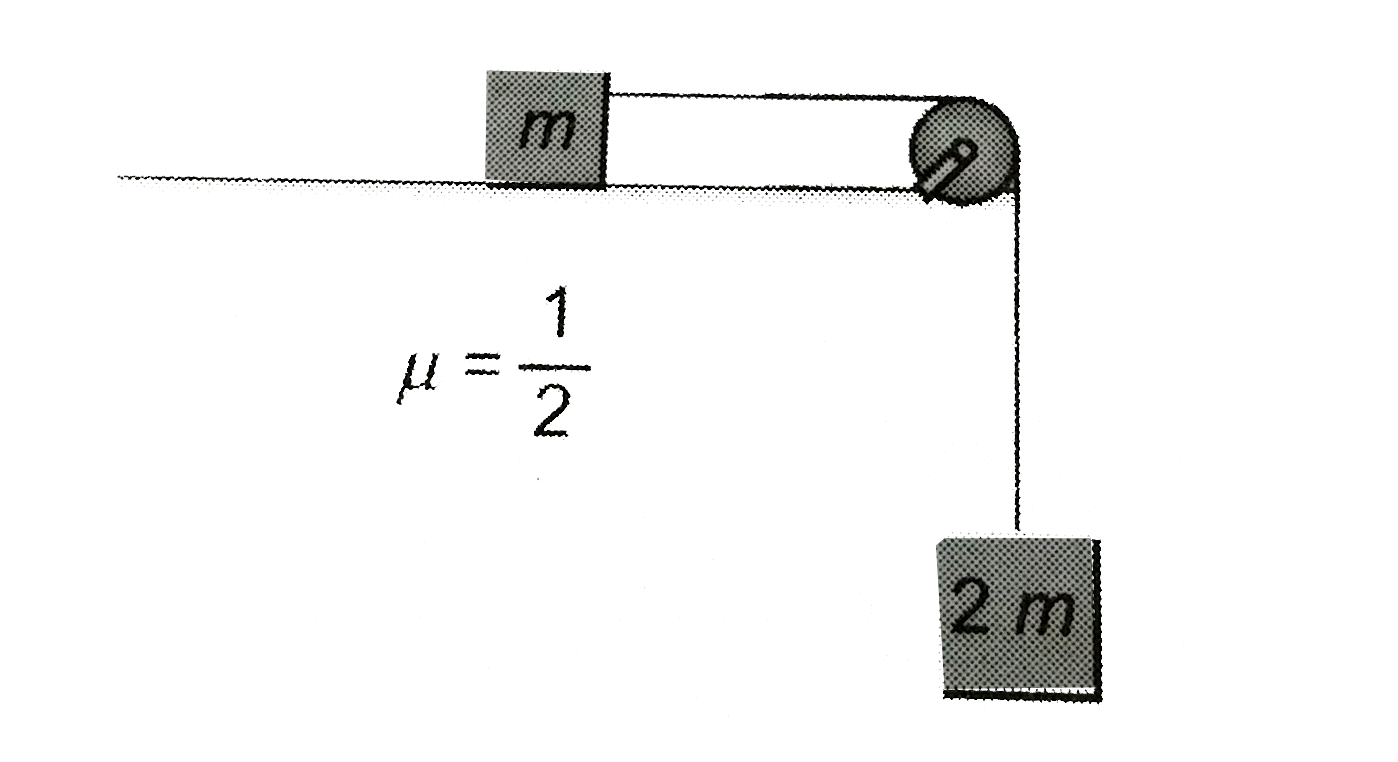
Consider the situation as shown in the figure. The system is released from rest. Find the speed of m when it has traveled a distance d on a rough surface.
View SolutionA solid uniform sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls without sliding along the surface. If the rim of the hemisphere is kept horizotnal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
View Solution
Knowledge Check

A small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere isA(3/7)mgB(9/7)mgC(13/7)mgD(17/7)mgA solid spherical ball of mass m is released from the topmost point of the shown semi - spherical shell. The track is sufficiently rough to enablle to enable pure rolling motion. The normal force between the ball and the shell at the lowest position is
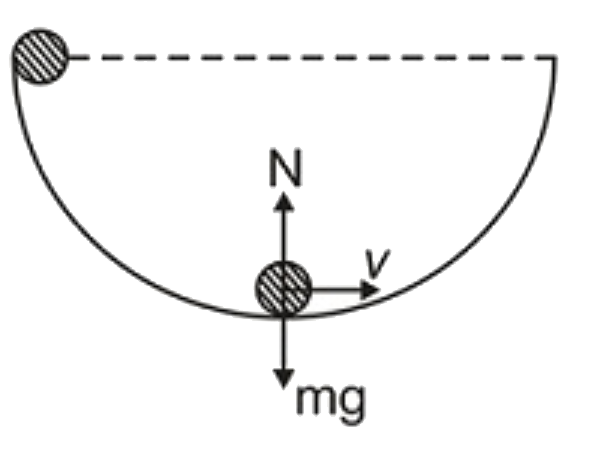 A127mgB79mgC177mgD107mg
A127mgB79mgC177mgD107mg
Consider the situation as shown in the figure. The boy of mass M holds the light rope and the system is at rest. If m is mass of the box, find the force exerted by the boy on the rope and contact force beteween the boy and the box.

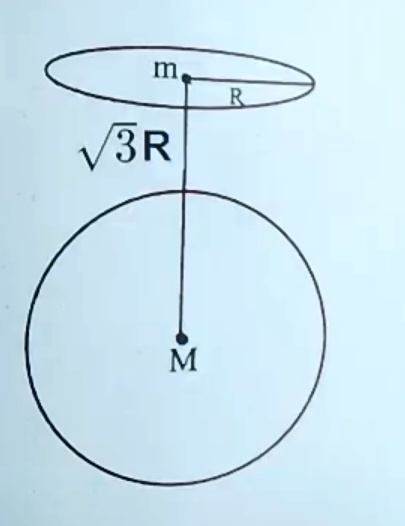
View SolutionFind the force of attraction between a solid sphere of mass M and a ring of mass m as shown.
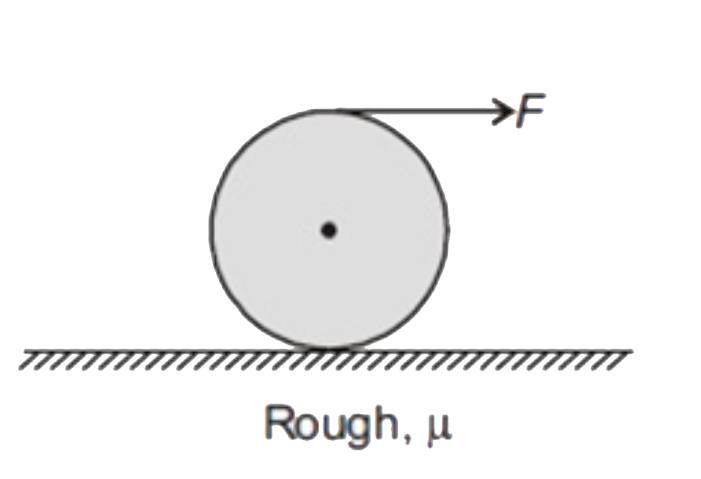
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
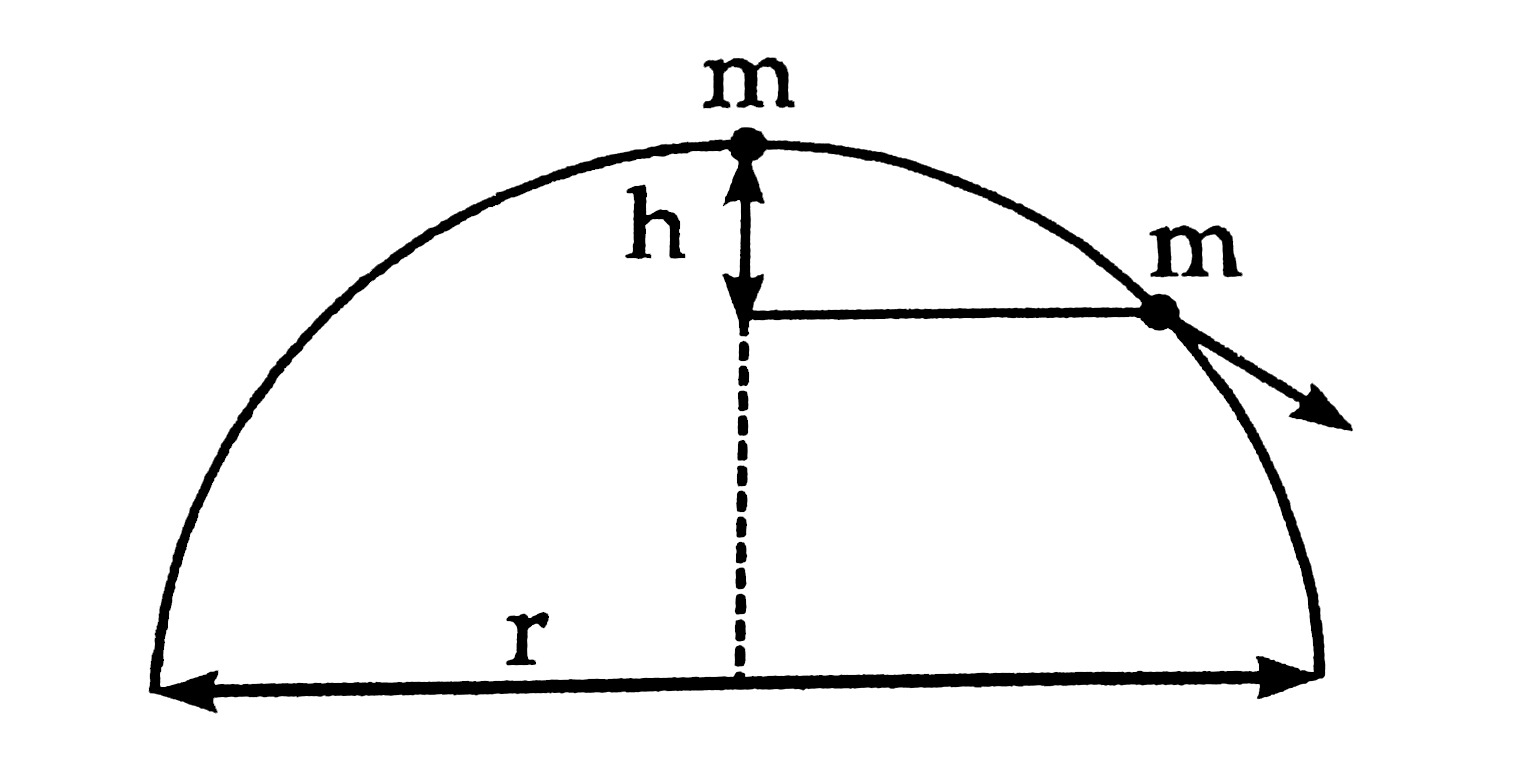
View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionIn the system shown in figure, the block A is released from rest. Find
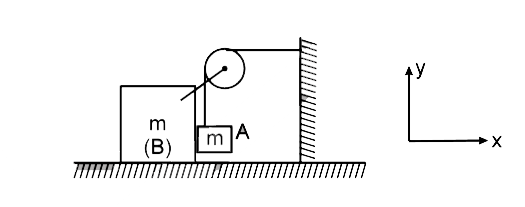
Contact force between ‘A’ and ‘B’.
View SolutionTwo uniform solid spheres of equal radii R, but mass M. and 4M have a centre to centre separation 6R, as shown in the figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. If the minimum speed v of the projectile so that it reaches the surface of the second sphere is √xGMyR, then find (x,+y).
'(##CEN_KSR_PHY_JEE_C10_038_Q05##)'
View Solution
