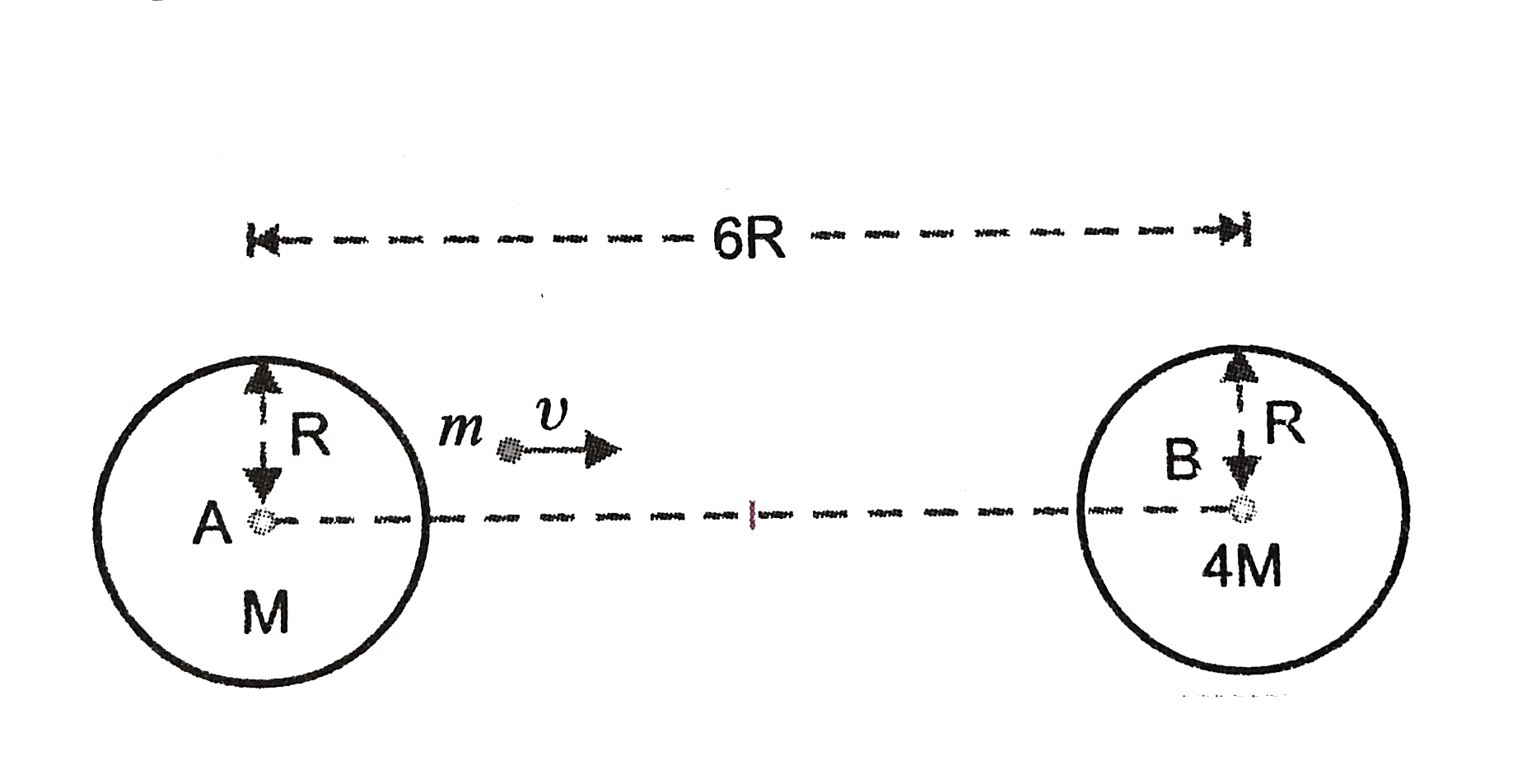
Two uniform solid spheres of equal radii R, but mass M. and 4M have a centre to centre separation 6R, as shown in the figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. If the minimum speed v of the projectile so that it reaches the surface of the second sphere is √xGMyR, then find (x,+y).
'(##CEN_KSR_PHY_JEE_C10_038_Q05##)'
The correct Answer is:8
Topper's Solved these Questions
Similar Questions
Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
View SolutionTwo uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of massm is projected from the surface of the sphere of mass M directly towards the centre of teh second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.

View Solution
Knowledge Check
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
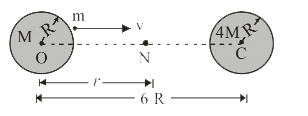 A√45GMRB√54GMRC√35GMRD√53GMR
A√45GMRB√54GMRC√35GMRD√53GMRThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzeroThree solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
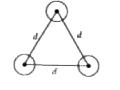 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
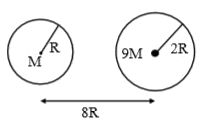
Suppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
View SolutionIf a particle of mass 'm' is projected from a surface of bigger sphere of mass '16M' and radius '2a' then find out the minimum velocity of the particle such that the particle reaches the surface of the smaller sphere of mass M and radius 'a'. Given that the distance between the centres of two spheres is 10 a.
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
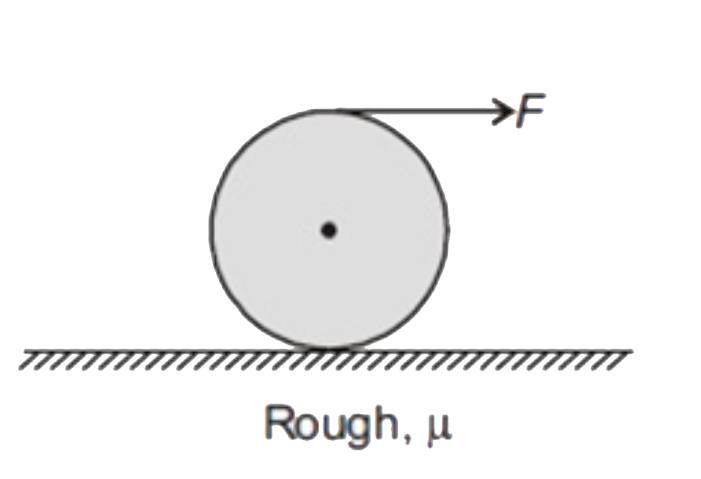
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View Solution
