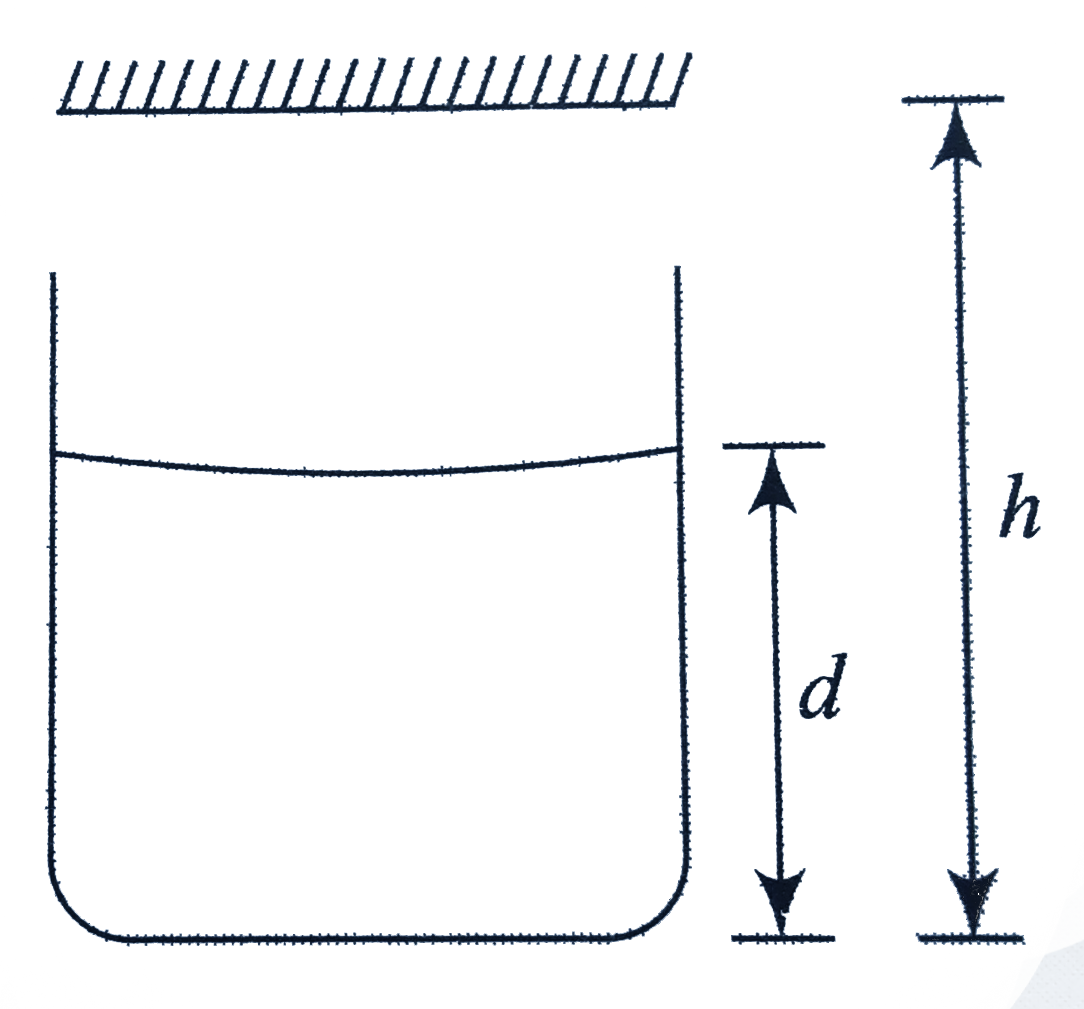
Consider the situation shown in figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) up of a bottom formed by the mirror.
The bottom of the beker appears to be shifted up by a distance
△t=(1−1μ)d
Thus, the apparent distance of the bottom from the mirror is h△t=h−(1−1μ)d=h−d+dμ. The image is formed behind the mirror at a distance h−d+dμ
Similar Questions
Consider the situation shown in Figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) upto a height d. Find the position of the image of bottom formed by the mirror.
View SolutionIn Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
View Solution
Knowledge Check
- Question 1 - Select One
Consider the situation shown in figure. Water (μ=4/3) is filled in a beaker up to a height of 10cm.
A plane mirror is fixed at a height of 5 cm from the surface of water. Distance of image from the mirror after reflection from it of an object O at the bottom of the beaker is
A15cmB12.5cmC7.5cmD10cm - Question 2 - Select One
Consider the situation shown in figure. Water (μw=43) is filled in a breaker upto a height of 10 cm. A plane mirror is fixed at a height of 5 cm from the surface of water. Distance of image from the mirror after reflection from it if an object O at the bottom of the beaker is
A15 cmB12.5cmC7.5cmD10 cm - Question 3 - Select One
Consider the situation shown in figure. Water (μW=43) is filled in a breaker upto a height of 10 cm . A plane mirror fixed at a height of 5 cm from the surface of water. Distance of image from the mirror after reflection from it of an object O at the bottom of the beaker is
A15 cmB12.5 cmC7.5 cmD10 cm
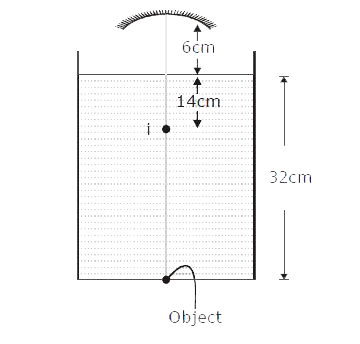
A beaker contains water (μ=4/3) filled to a height of 32 cm. A concave mirror is fixed 6 cm above the surface of water as shown in figure. An object is placed at the bottom of the beaker and its image is formed 14 cm below the surface of water. The focal length of the mirror is
View SolutionConsider a tin can of height h as shown in the figure. A coin lies on the botttom at the centre. From the position shown you can barely see the far side of the bottom of the can. When the can is slowly filled with water of refractive index μ, coin is just visible when the can is full. Show that the ratio of the height to radius is
hr=2√μ2−14−μ2
View SolutionConsider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is mu. (a) At what distance(s) from itself will the fish see the image(s) of the eye ? (b) At what distance(s) from itself will the eye see the image(s) of the fish. (11-T
View SolutionConsider the situation in figure. The bottom of the pot is reflecting plane mirror , S is small fish is a human eye . Refractive index of water is μ. Fish can see two images of human eye , first due to refractive only and other due to refraction and than reflection . Distance of these images from fish are S1andS2 respectively . Human eye can also see the two images of fish, first due to refraction only and other due to reflection and then refraction . Distance of these images from human eye are S3andS4 respectively . Match the quantities of column-I (with their value in column-(II)
_E01_093_Q01.png)
Column IColumn II(A)S1(p)H[1+12μ](B)S2(q)H[μ+12](C)S3(r)H[1+32μ](D)S4(s)H[μ+32]View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
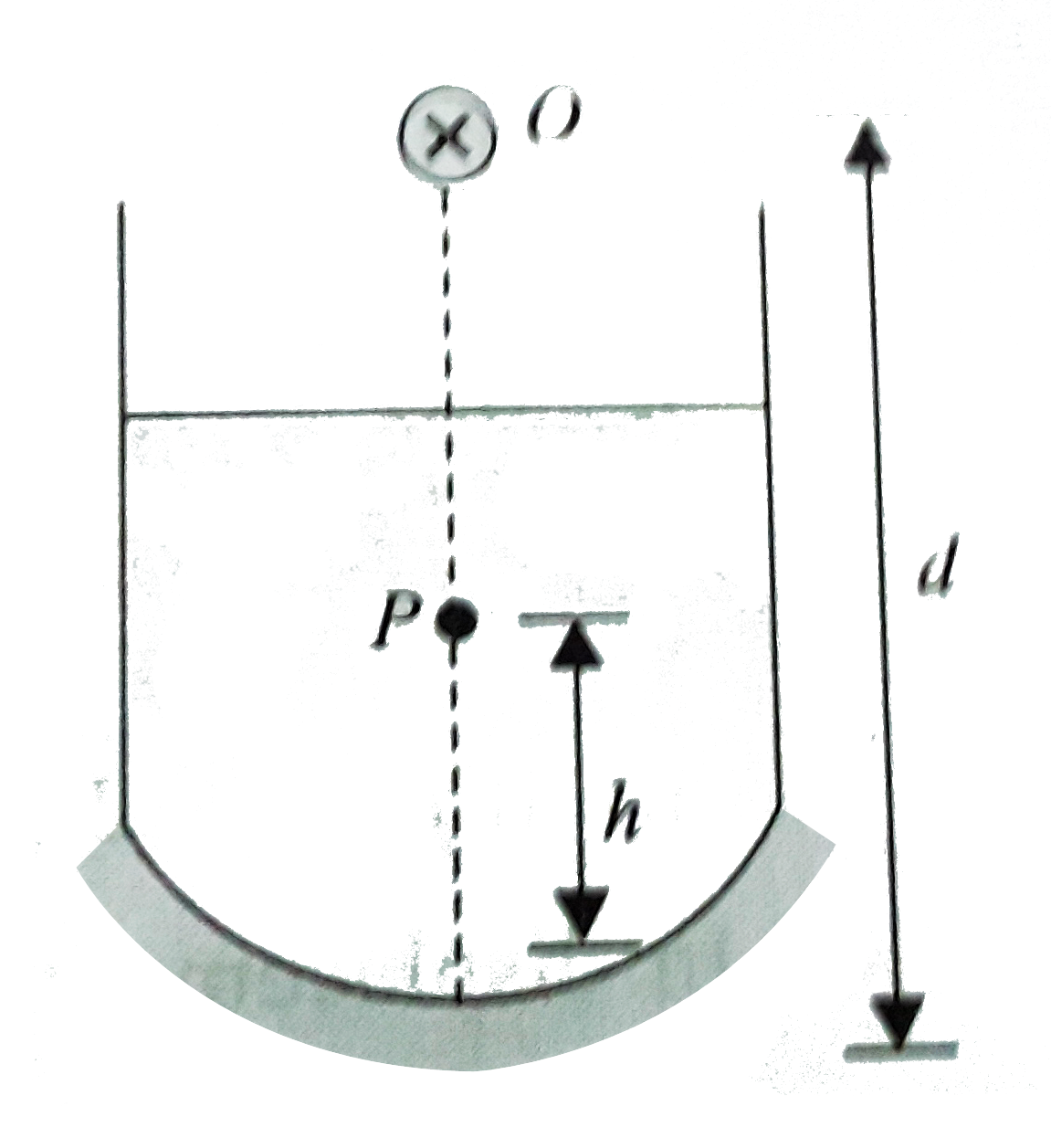
View Solution