Consider the system of weights P(1)=1 kg,P(2) = 2 kg,P(3) = 5kg and P(

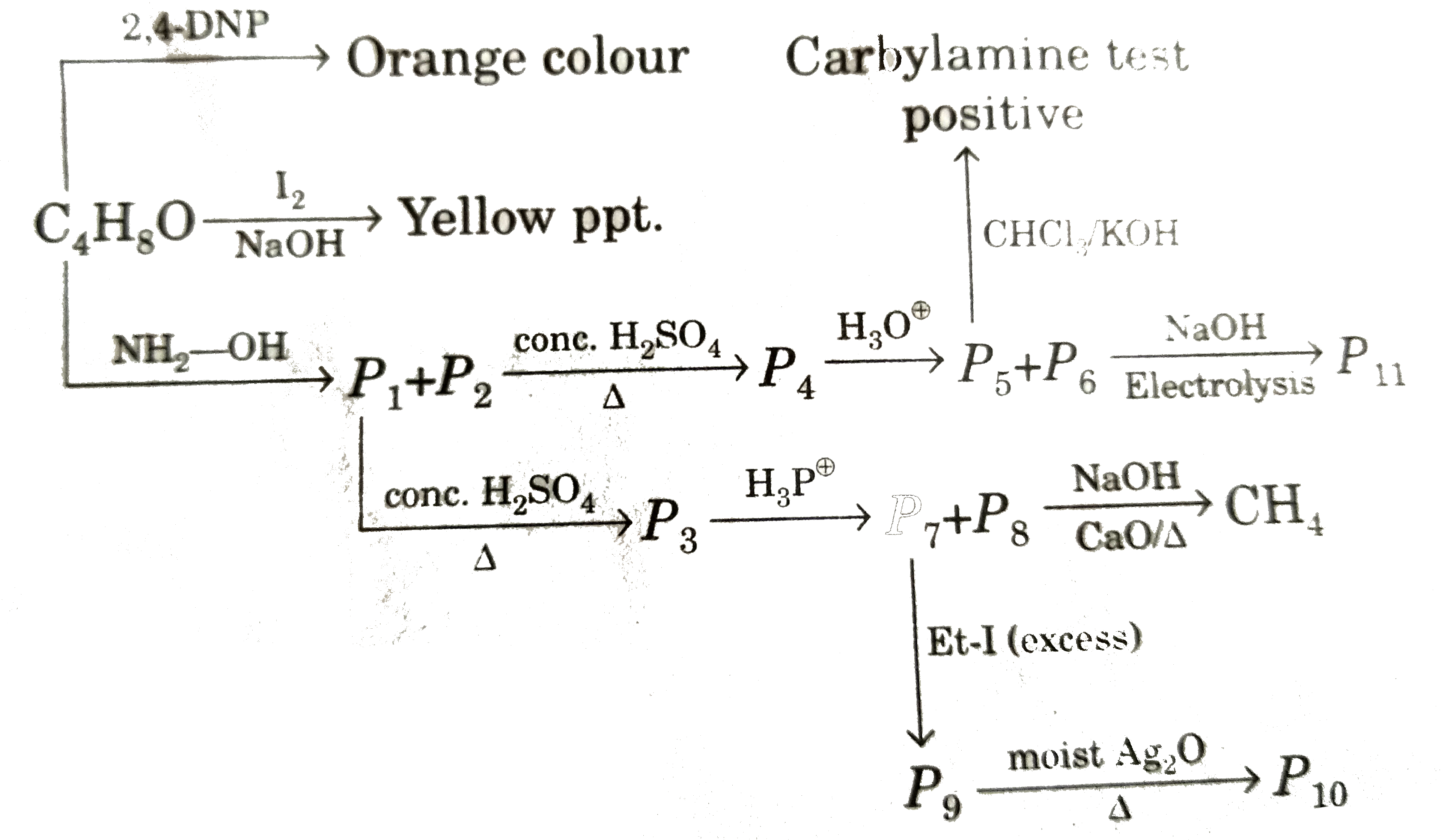
What is the relationship between $P_{1}$ and $P_{2}$
AGeometrical isomers
BOptical isormers
CPositional isomers
DChain isomers
A block of mass m = 1 kg is placed over a plank Q of mass M = 6 kg, placed over a smooth horizontal surface as shown in figure. Block P is given a velocity $v = 2 m / s^{2}$ to the right. If the coefficient of friction between P and Q is $μ = 0.3$ . Find the acceleration of Q relative to P.

A $4 m / s^{2}$
B $3.5 m / s^{2}$
C $2 m / s^{2}$
D $10.0 m / s^{2}$
$P_{1} : x + 3 y - z = 0 and P_{2} : y + 2 z = 0$ are two intersecting planes $P_{3}$ is a plane passing through the point (2,1,-1) and through the line of intersection of $P_{1} and P_{2}$

The angle between $P_{1} and P_{2}$ is ________.
A ${cos}^{- 1} (\frac{1}{5})$
B ${cos}^{- 1} (\frac{1}{\sqrt{55}})$
C ${cos}^{- 1} (\frac{2}{\sqrt{11}})$
D ${cos}^{- 1} (\frac{3}{\sqrt{11}})$

The correct Answer is: $6.87 m s^{- 2}$ (b) $8.83 N, 16.12 N$ (c) 1.465 N