Considering the earth as a short magnet with its centre coinciding with the centre of earth, show that the angle of dipϕis related to magnetic latitude λ by the relation tanϕ=2tanλ.
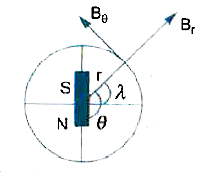
consider the situation as shown in the figure . For dipole , at position (r,θ) we have
Br=μ04π2Mcosθr3andB0=μ04πMsinθr3 .......... (1)
and as tanϕ=BVBH=−BrBθ, so in the light of eq (1) ,
tanϕ=−2cotθ
But from figure θ=90+λ
so , tanϕ=−2cot(90+λ) , i.e., thanϕ=2tanλ.
Topper's Solved these Questions
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - EXERCISE (LONG ANSWER QUESTIONS )
6 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )
6 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
Similar Questions
Knowledge Check
Let the magnetic field on earth be modeled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator is
Aalways zeroBpositive, negative or zeroCunboundedDalways negativeConsider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators Obtain the declination and dip angles at P and Q.
A0∘,11.3∘B11.3∘,0∘C11.3∘,11.3∘D0∘,0∘
Weight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Difference between Weight Wr and the gravitational attraction on the body can be given as
View SolutionA very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
View SolutionLet the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator
View SolutionA short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14cm from the centre of the magnet. The earth's magnetic field at the plane is 0⋅36G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null points (i.e. 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and apposite to the horizontal component of earth's magnetic field).
View SolutionTwo coils each of 100 turns are held such that one lies in vertical plane and the other in the horizontal plane with their centres coinciding. The radius of the vetical coil is 0.20m and that of the horizontal coil is 0.30m. How will you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal component of earth's magnetic field =0.35×10−4T and angle of dip =30∘.
View SolutionConsider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators Obtain the declination and dip angles at P and Q.
View Solution
