Magnetic field arises due to charges in motion. Can a system have magnetic moments even though its net charge is zero?
To determine whether a system can have a magnetic moment even if its net charge is zero, we can analyze the concept of magnetic moments and how they arise from moving charges.
1. Understanding Magnetic Moment:
- The magnetic moment (μ) of a system is defined as the product of the current (I) flowing through a loop and the area (A) of that loop. Mathematically, it can be expressed as:
μ=I⋅A
- Here, current is defined as the charge (Q) passing through a point per unit time (T):
I=QT
2. Considering a System with Zero Net Charge:
- Let's consider a simple system with two charges, +Q and −Q, rotating in circular paths of different radii. For example, one charge is rotating in a circle of radius r1 and the other in a circle of radius r2.
3. Calculating Current for Each Charge:
- The current produced by each charge depends on its velocity and the time period of rotation. If the velocities are V1 and V2, and the time periods are T1 and T2, the currents can be expressed as:
I1=QT1,I2=QT2
4. Determining the Area of Each Loop:
- The area for each circular path can be calculated as:
A1=πr21,A2=πr22
5. Calculating the Magnetic Moment for Each Charge:
- The magnetic moment for each charge can be calculated as:
μ1=I1⋅A1=(QT1)⋅(πr21)
μ2=I2⋅A2=(QT2)⋅(πr22)
6. Net Magnetic Moment:
- The total magnetic moment of the system is the vector sum of the individual magnetic moments. Since the charges are opposite, the net magnetic moment will depend on the magnitudes and directions of μ1 and μ2. Therefore, the net magnetic moment can be expressed as:
μnet=μ1+μ2
- It is possible for μnet to be non-zero even if the net charge of the system is zero.
7. Conclusion:
- A system can indeed have a magnetic moment even if its net charge is zero. This is commonly observed in materials such as paramagnetic substances, where individual atomic magnetic moments contribute to a net magnetic moment despite the overall charge neutrality.
- The magnetic moment (μ) of a system is defined as the product of the current (I) flowing through a loop and the area (A) of that loop. Mathematically, it can be expressed as:
μ=I⋅A
- Here, current is defined as the charge (Q) passing through a point per unit time (T):
I=QT
- Let's consider a simple system with two charges, +Q and −Q, rotating in circular paths of different radii. For example, one charge is rotating in a circle of radius r1 and the other in a circle of radius r2.
- The current produced by each charge depends on its velocity and the time period of rotation. If the velocities are V1 and V2, and the time periods are T1 and T2, the currents can be expressed as:
I1=QT1,I2=QT2
- The area for each circular path can be calculated as:
A1=πr21,A2=πr22
- The magnetic moment for each charge can be calculated as:
μ1=I1⋅A1=(QT1)⋅(πr21)
μ2=I2⋅A2=(QT2)⋅(πr22)
- The total magnetic moment of the system is the vector sum of the individual magnetic moments. Since the charges are opposite, the net magnetic moment will depend on the magnitudes and directions of μ1 and μ2. Therefore, the net magnetic moment can be expressed as:
μnet=μ1+μ2
- It is possible for μnet to be non-zero even if the net charge of the system is zero.
- A system can indeed have a magnetic moment even if its net charge is zero. This is commonly observed in materials such as paramagnetic substances, where individual atomic magnetic moments contribute to a net magnetic moment despite the overall charge neutrality.
Topper's Solved these Questions
Similar Questions
Suppose that an electric charge moves in a magnetic field in a plane perpendicular to the lines of induction. Prove that the orbital magnetic moment of the circulating charge is directed against the field.
View SolutionAssertion (A): The earth's magnetic field is due to iron present in its core.
Reason (R ): At a high tempeature magnet losses its magnetic property or magnetism.
View SolutionFerromagnetism arises because of the spontaneous alignment of the magnetic moments due to unpaired electrons as
View SolutionA particule having charge q enters a rection of untiormal magnetic field B (direction inwards) and in denfectro as shown . The magnetic of the momentum of the particles is
View SolutionA: A system can have magnetic moments even though its net charge is zero.
R: Magnetic moment is created by charges in motion.
View SolutionA: The magnetic field always accelerates a moving charge if the moving charge cuts the field lines.
R: When a moving charge cuts the magnetic field lines, the magnetic force on the charge is always non zero.
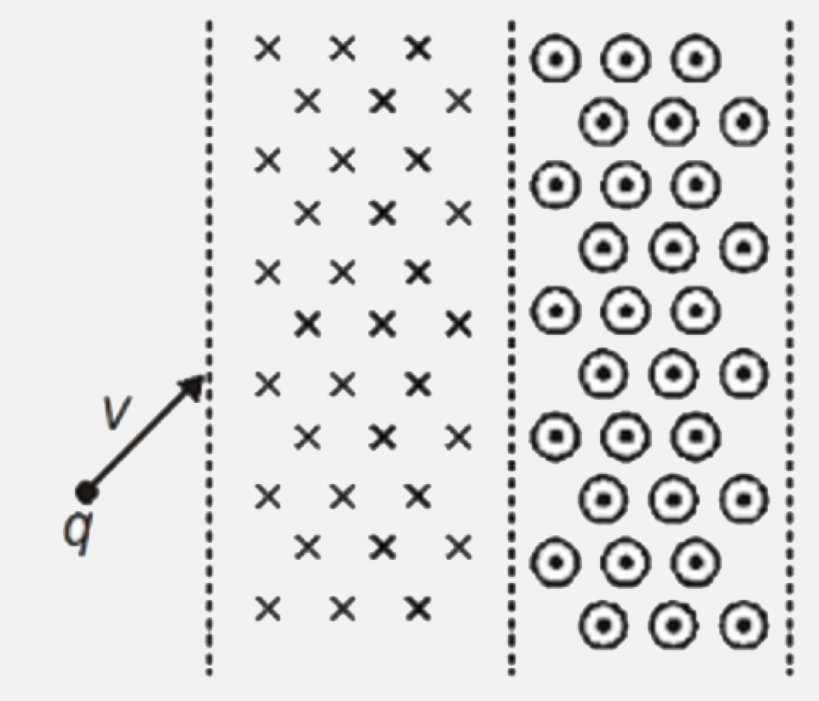
View SolutionA positive charge enters in the region of transverse magnetic field as shown in figure. Velocity of charge is in such a way that charge passes through both inward and outward magnetic field regions, then possibly correct path of the charge is
View SolutionStatement-1 A current carrying wire is placed parallel to magnetic field. The force on it due the magnetic field is zero
Statement-2 The net charge on current wire is zero
View SolutionA charge is moving through a magnetic field. The force acting on the charge is maximum when the angle between the velocity of charge and the magnetic field is _______
View SolutionAssertion In non-uniform magnetic field speed of a charged particle varies.
Reason Work done by magnetic force on a charged particle is always zero.
View Solution
