Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
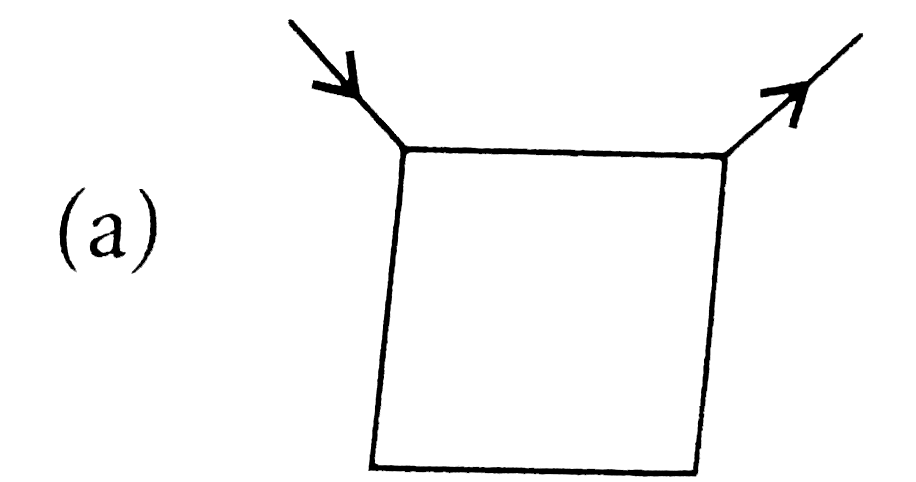
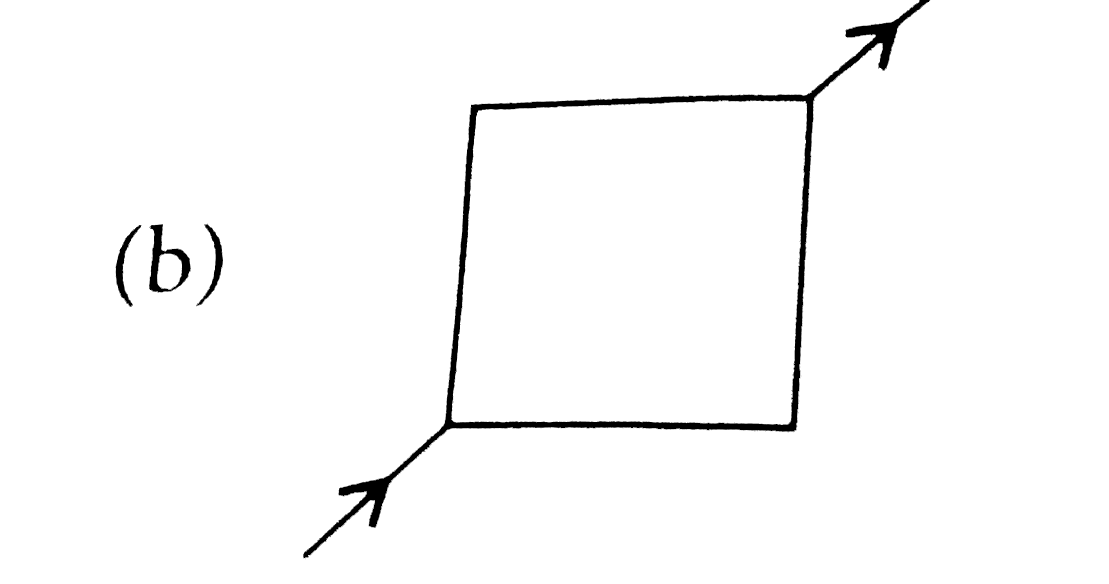
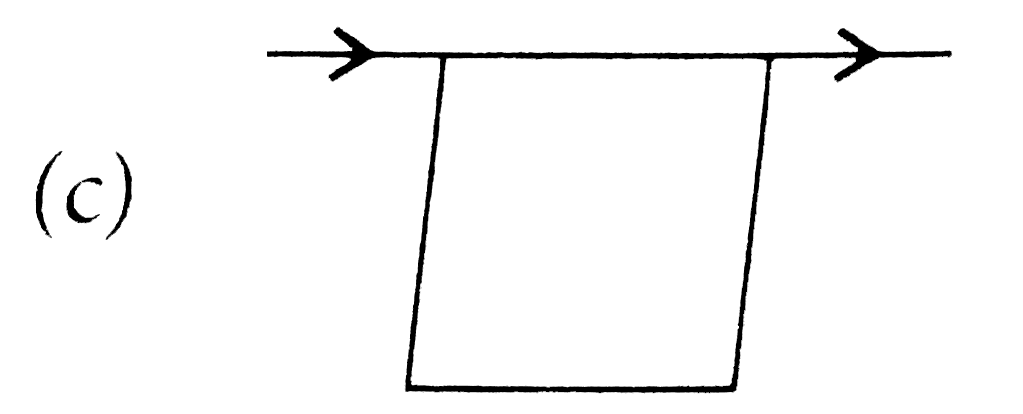
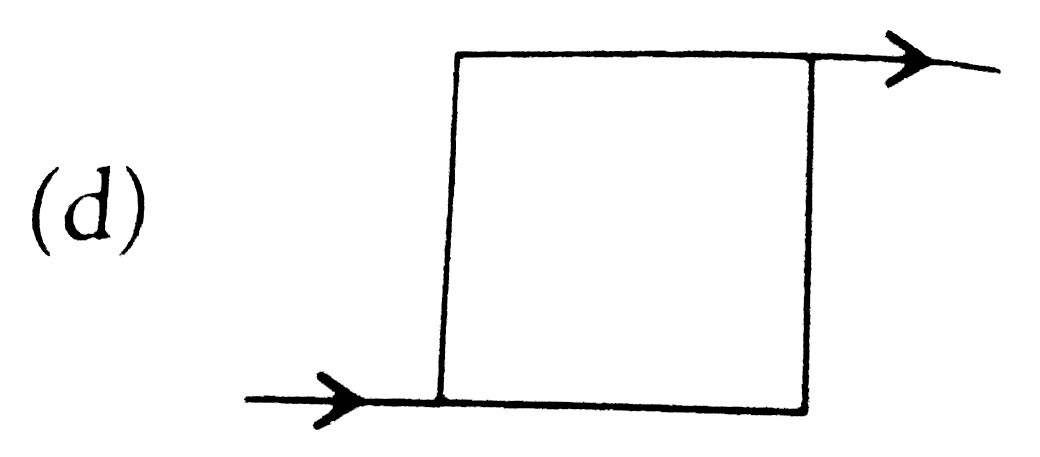
The correct Answer is:C
To determine in which case the magnetic field at the center of a uniform square frame is not zero, we can analyze the situation step by step.
1. Understanding the Configuration:
- We have a uniform square frame through which current is flowing. The magnetic field at the center of the frame depends on the direction of the current in relation to the center point.
2. Analyzing Case A:
- In this case, if the current flows along one side of the square frame and we extend that line, the center point lies directly on the same axis as the current.
- According to the Biot-Savart law, the magnetic field produced by a straight current-carrying conductor at a point on its axis is zero.
- Conclusion: The magnetic field at the center is zero.
3. Analyzing Case B:
- Similar to Case A, if the current flows along another side of the square frame and we extend that line, the center point again lies on the same axis as the current.
- Again, the magnetic field at the center will be zero for the same reason as in Case A.
- Conclusion: The magnetic field at the center is zero.
4. Analyzing Case C:
- In this case, if the current flows in a way that it creates a loop around the center, the magnetic field at the center can be determined using the right-hand thumb rule.
- The right-hand thumb rule states that if you curl the fingers of your right hand in the direction of the current, your thumb points in the direction of the magnetic field.
- Here, the magnetic field at the center will point inward, and it will have a non-zero value.
- Conclusion: The magnetic field at the center is not zero.
5. Analyzing Case D:
- If there are two wires carrying current in opposite directions, the magnetic fields produced by each wire at the center will cancel each other out.
- The net magnetic field at the center will be zero because the magnitudes are equal and the directions are opposite.
- Conclusion: The magnetic field at the center is zero.
Final Answer:
The magnetic field at the center of the square frame is not zero in Case C.
- We have a uniform square frame through which current is flowing. The magnetic field at the center of the frame depends on the direction of the current in relation to the center point.
- In this case, if the current flows along one side of the square frame and we extend that line, the center point lies directly on the same axis as the current.
- According to the Biot-Savart law, the magnetic field produced by a straight current-carrying conductor at a point on its axis is zero.
- Conclusion: The magnetic field at the center is zero.
- Similar to Case A, if the current flows along another side of the square frame and we extend that line, the center point again lies on the same axis as the current.
- Again, the magnetic field at the center will be zero for the same reason as in Case A.
- Conclusion: The magnetic field at the center is zero.
- In this case, if the current flows in a way that it creates a loop around the center, the magnetic field at the center can be determined using the right-hand thumb rule.
- The right-hand thumb rule states that if you curl the fingers of your right hand in the direction of the current, your thumb points in the direction of the magnetic field.
- Here, the magnetic field at the center will point inward, and it will have a non-zero value.
- Conclusion: The magnetic field at the center is not zero.
- If there are two wires carrying current in opposite directions, the magnetic fields produced by each wire at the center will cancel each other out.
- The net magnetic field at the center will be zero because the magnitudes are equal and the directions are opposite.
- Conclusion: The magnetic field at the center is zero.
The magnetic field at the center of the square frame is not zero in Case C.
Topper's Solved these Questions
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 3
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 1
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT Exemplar
Explore 11 Videos
Similar Questions
The magnetic field at the centre of square of side a is
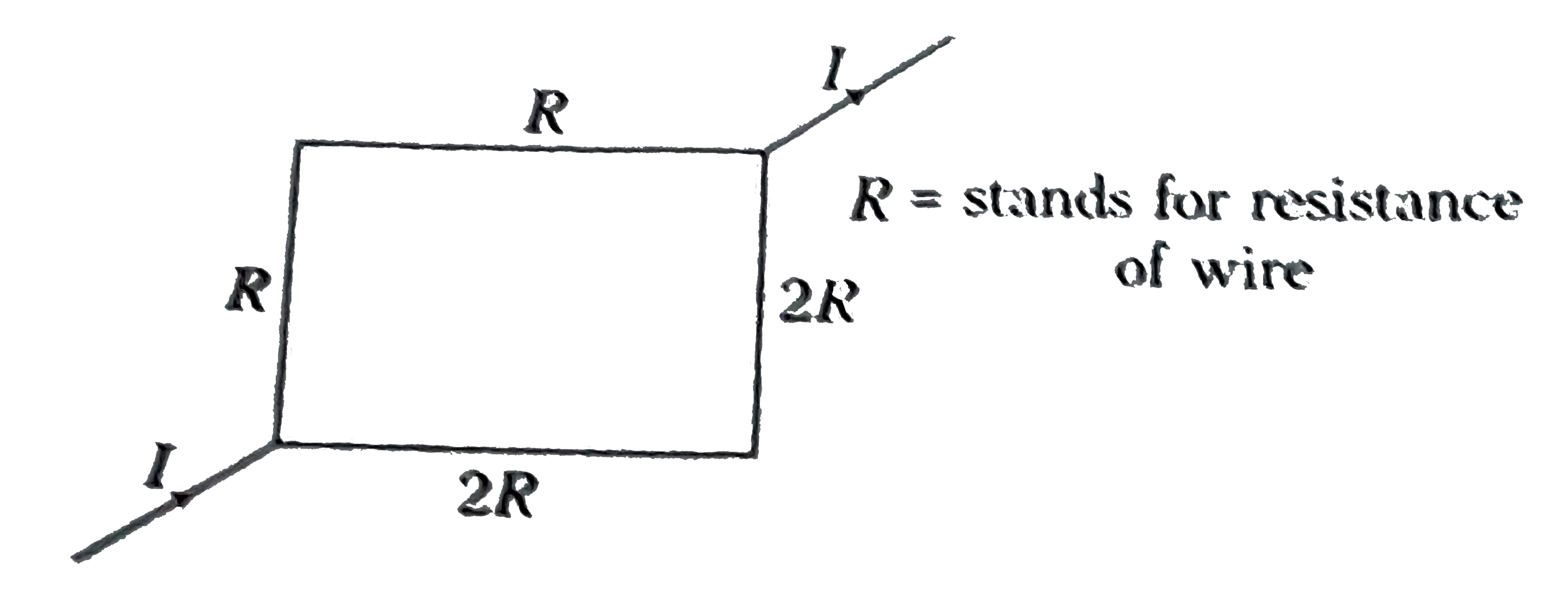
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
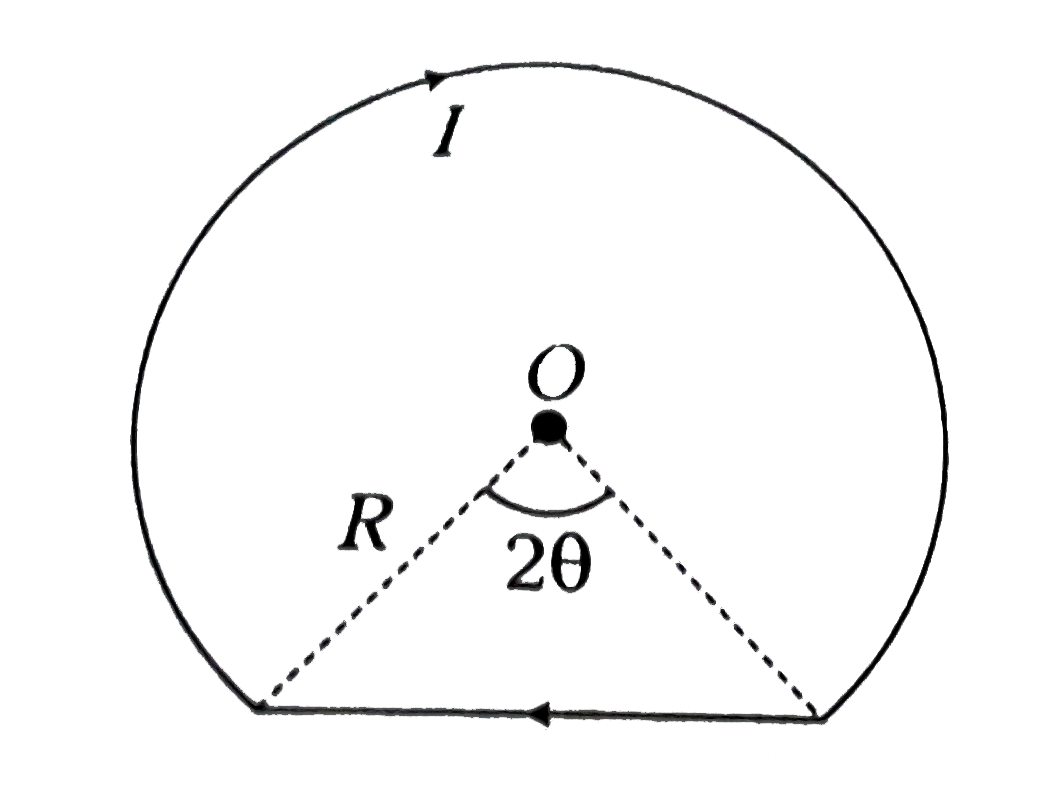
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
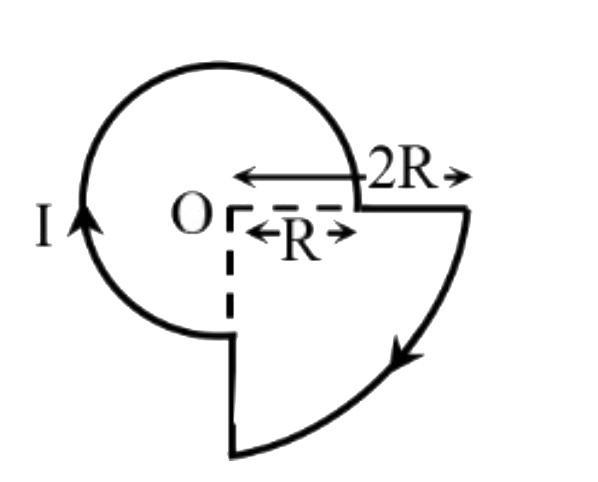
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
View SolutionIf current through a circular coil flows in clockwise direction, then the direction of magnetic field at the centre of the circular coil is………………to the plane of the coil, directed……………. .
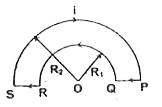
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionFour very long wires are arranged as shown in the figure, so that their cross - section forms a square, with connections at the ends so that current I flow through all four wires. Length of each side of the formed such square is b. The magnetic field at the central point P (centre of the square) is
View Solution