Two identical magnetic dipoles of magnetic moments 1⋅0Am2 each are placed at a separation of 2m with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
√5×10−7T
5×10−7T
√2×10−7T
10−7T
The correct Answer is:A
To solve the problem of finding the resultant magnetic field at a point midway between two identical magnetic dipoles, we can follow these steps:
Step 1: Understand the Configuration
We have two magnetic dipoles, each with a magnetic moment m=1A m2, placed at a separation of 2m. The axes of the dipoles are perpendicular to each other. We need to find the magnetic field at the midpoint between the two dipoles.
Step 2: Calculate the Magnetic Field from Each Dipole
The magnetic field due to a dipole at a point along its axis is given by the formula:
Baxis=μ04π⋅2md3
where μ0=4π×10−7T m/A is the permeability of free space, m is the magnetic moment, and d is the distance from the dipole to the point where the field is being calculated.
Step 3: Calculate B1 (Field from Dipole 1)
Since the midpoint is 1m away from Dipole 1:
B1=μ04π⋅2m(1)3=10−71⋅2⋅1=2×10−7T
This field is directed away from Dipole 1.
Step 4: Calculate B2 (Field from Dipole 2)
For Dipole 2, which is also 1m away from the midpoint:
B2=μ04π⋅m(1)3=10−71⋅1=1×10−7T
This field is directed towards Dipole 2.
Step 5: Determine the Direction of the Fields
Since the dipoles are perpendicular to each other:
- B1 is directed along the axis of Dipole 1.
- B2 is directed along the axis of Dipole 2.
Step 6: Calculate the Resultant Magnetic Field
The resultant magnetic field Bnet can be found using the Pythagorean theorem since the fields are perpendicular:
Bnet=√B21+B22
Substituting the values:
Bnet=√(2×10−7)2+(1×10−7)2
Bnet=√4×10−14+1×10−14=√5×10−14=√5×10−7T
Step 7: Final Result
Thus, the resultant magnetic field at the midpoint between the dipoles is:
Bnet=√5×10−7T
We have two magnetic dipoles, each with a magnetic moment m=1A m2, placed at a separation of 2m. The axes of the dipoles are perpendicular to each other. We need to find the magnetic field at the midpoint between the two dipoles.
The magnetic field due to a dipole at a point along its axis is given by the formula:
Baxis=μ04π⋅2md3
where μ0=4π×10−7T m/A is the permeability of free space, m is the magnetic moment, and d is the distance from the dipole to the point where the field is being calculated.
Since the midpoint is 1m away from Dipole 1:
B1=μ04π⋅2m(1)3=10−71⋅2⋅1=2×10−7T
This field is directed away from Dipole 1.
For Dipole 2, which is also 1m away from the midpoint:
B2=μ04π⋅m(1)3=10−71⋅1=1×10−7T
This field is directed towards Dipole 2.
Since the dipoles are perpendicular to each other:
- B1 is directed along the axis of Dipole 1.
- B2 is directed along the axis of Dipole 2.
The resultant magnetic field Bnet can be found using the Pythagorean theorem since the fields are perpendicular:
Bnet=√B21+B22
Substituting the values:
Bnet=√(2×10−7)2+(1×10−7)2
Bnet=√4×10−14+1×10−14=√5×10−14=√5×10−7T
Thus, the resultant magnetic field at the midpoint between the dipoles is:
Bnet=√5×10−7T
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 150videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
Figure shows two identical magnetic dipoles aandb of magnetic moments M each, placed at a separation d, with their axes perpendicular to each other. Find the magnetic field at the point P midway between the dipoles.
 View Solution
View SolutionTwo identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
View Solution
Knowledge Check
- Question 1 - Select One
Two identical magnetic dipoles of magnetic moments 2Am2 are placed at a separation of 2m with their axes perpendicular to each other in air. The resultant magnetic field at a mid point between the dipole is
A4√5×10−5 TB2√5×10−5 TC4√5×10−7 TD2√5×10−7 T
Two identical short bar magnets of magnetic moment M each are placed at distance r apart in end-on position, then magnetic force between both is
View SolutionTwo identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View SolutionA bar magnet of magnetic moment M1 is axially cut into two equal parts. If these two pieces are arranged perpendiucular to each other, the resultant magnetic moment is M2.
Then the vale of M1M2 isView SolutionA bar magnet of magnetic moment M1 is axially cut into two equal parts. If these two pieces are arranged perpendiucular to each other, the resultant magnetic moment is M2.
Then the vale of M1M2 isView SolutionTwo magnets of moment M and 2 M are tied at an angle of 60∘ to each other . What is the resultant magnetic moment of the combination ?
View SolutionThree identical bar magnets each of magnetic moment M are arranged in the form of an equilateral triangle such that at two vertices like poles are in contact. The resultant magnetic moment will be
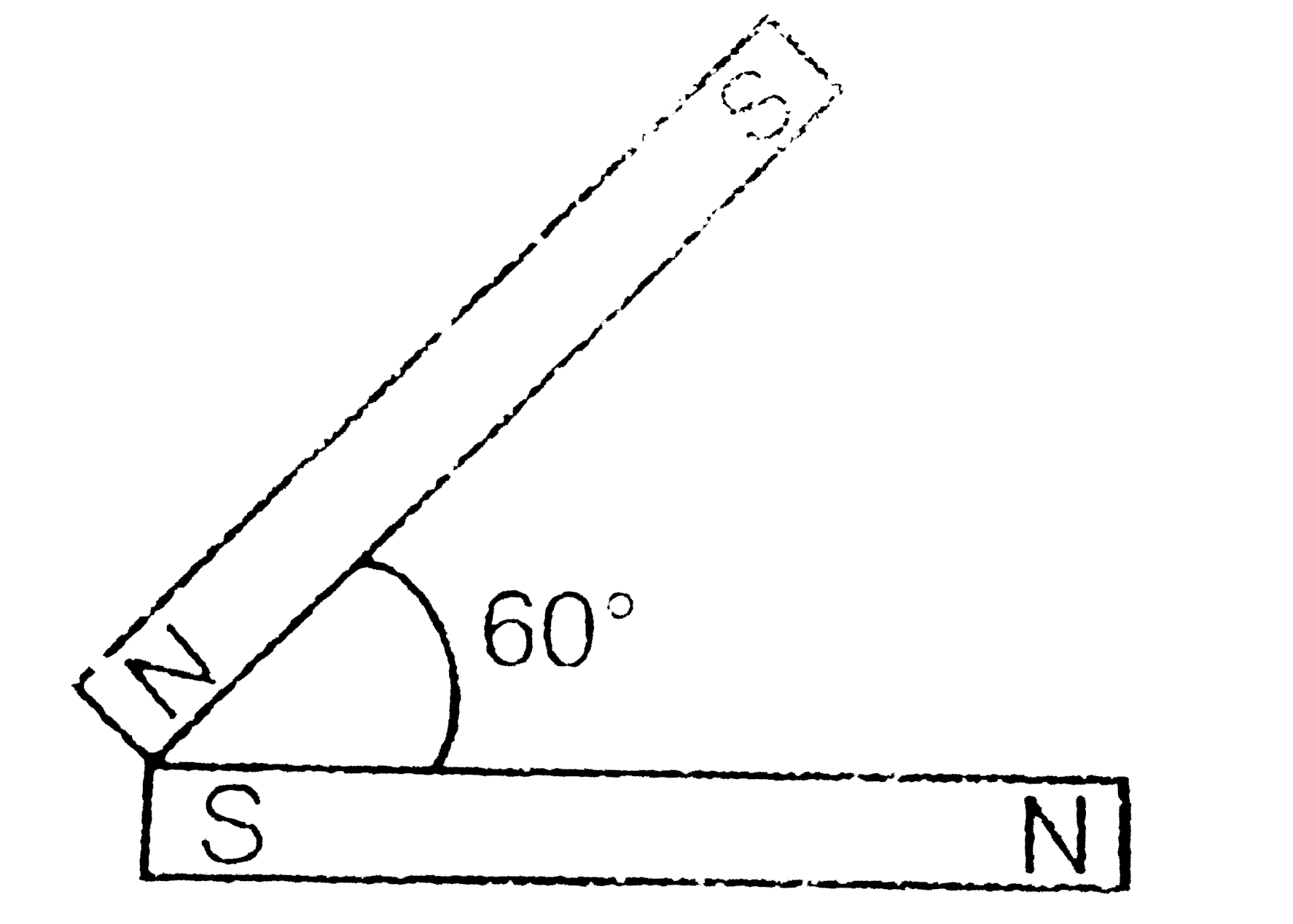
View SolutionTwo identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
 View Solution
View Solution

