Current I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

B=μ04πId(sinθ1+sinθ2)

here, d=rsin45∘=r√2
B=2×μ04πI(r√2)(sin45∘+sin90∘)
=2√2μ04πIr(1√2+1)=μ02πIr(√2+1)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
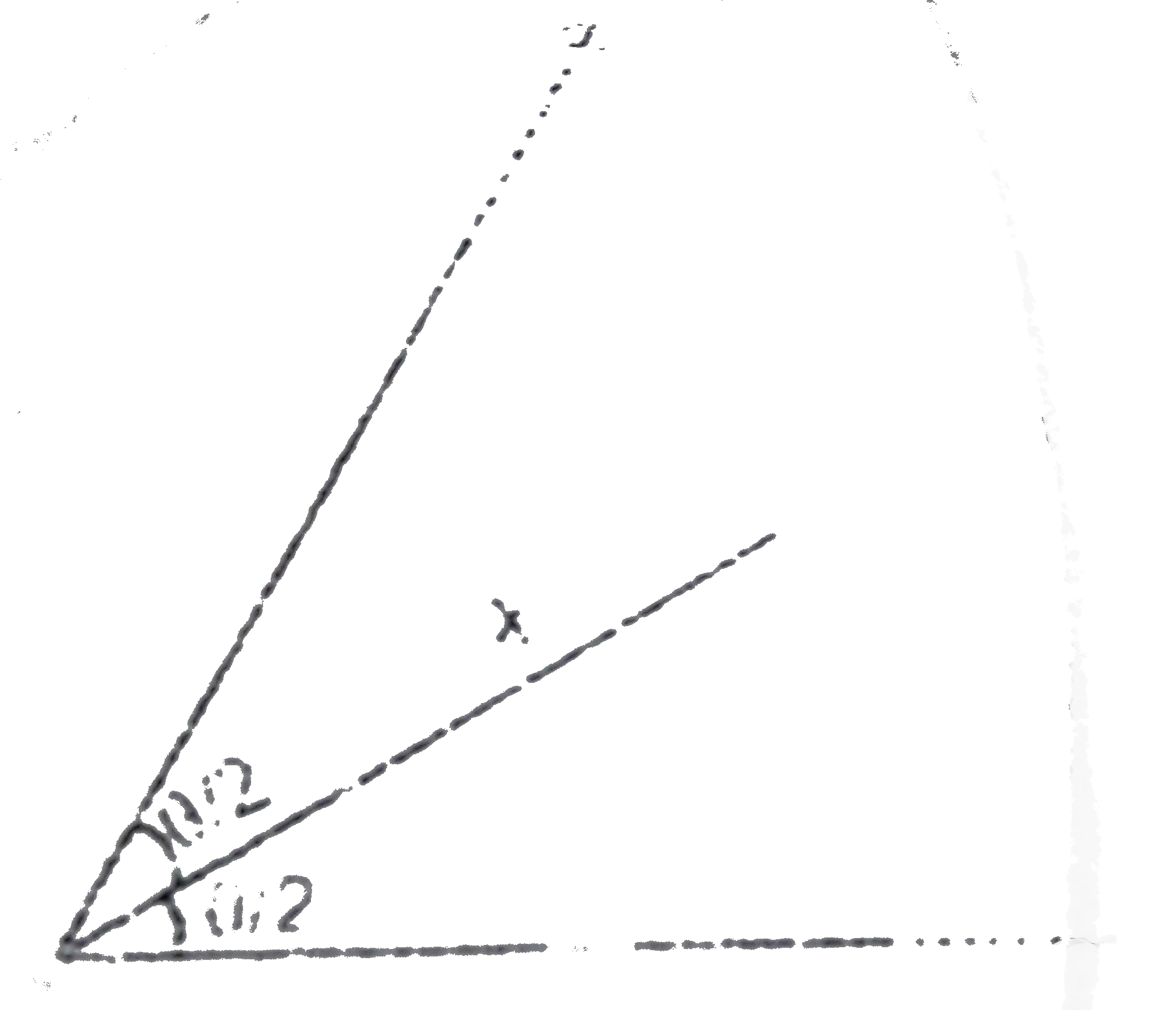 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙A long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)
 A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πd
A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πdFigure shows a long wire bent at the middle to from a right angle
 AThe magnitude of magnetic field at the points P, Q, R and S are same.BThe direction of magneitc field at points P and S are sameCThe magnitude of magnetic field at points P and S is zeroDThe direction of magnetic field at points R and S are opposite to each other.
AThe magnitude of magnetic field at the points P, Q, R and S are same.BThe direction of magneitc field at points P and S are sameCThe magnitude of magnetic field at points P and S is zeroDThe direction of magnetic field at points R and S are opposite to each other.
Alongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionFigure4.18 shows a current carrent carrying wire bent at an angle α. Find magentic induction at a point P located on the angle bisector at a distance x from the point O at the bend.

View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)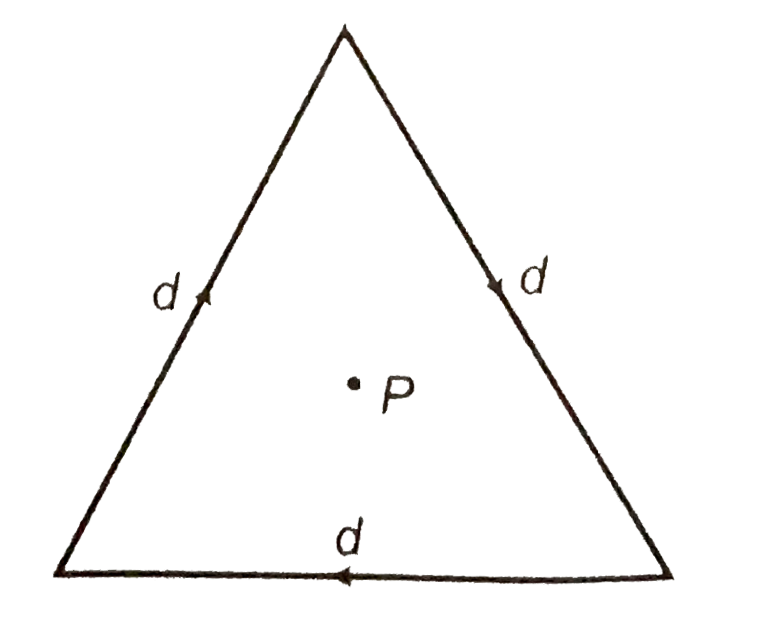
P is the centre of equilateral triangle.
(d)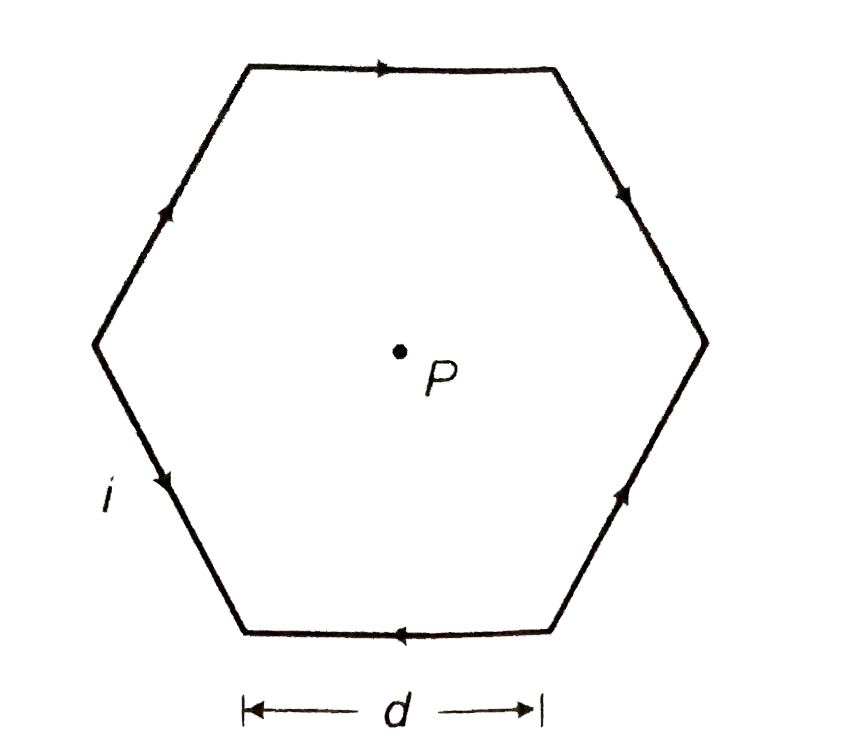
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)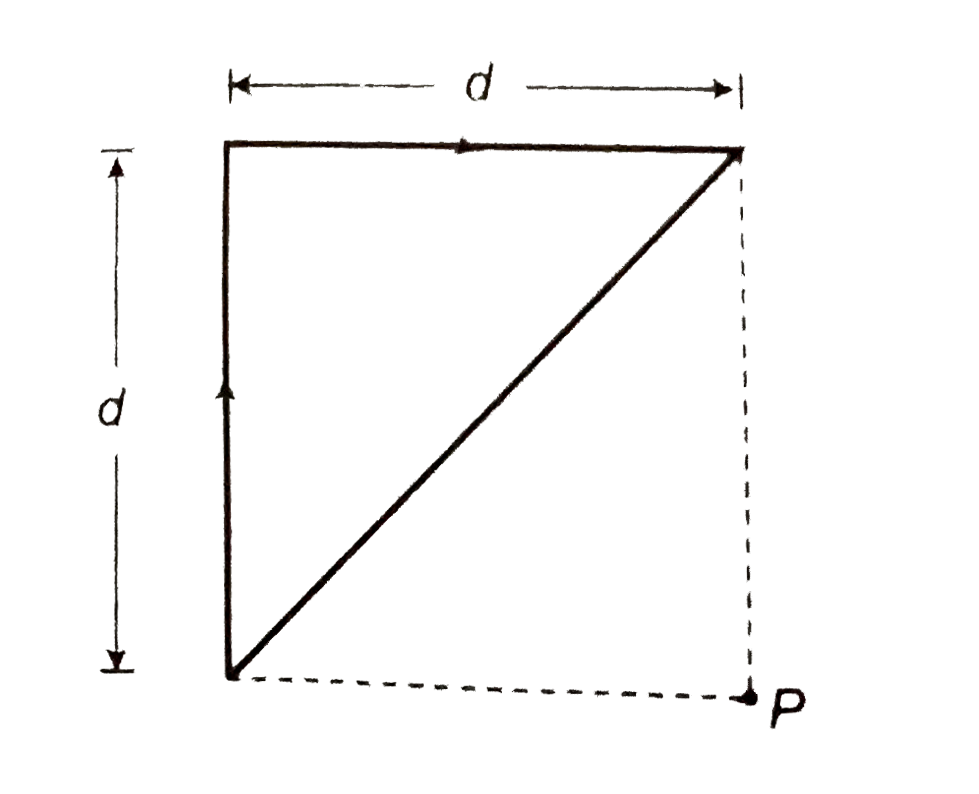
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View Solution3. Draw an obtuse-angled triangle and a right-angled triangle. Find the points of the concurrence of the angle bisectors of each angle
View Solution

