Deduce the expression for the equivalent resistance of there resistor connected in series.
Series connection :
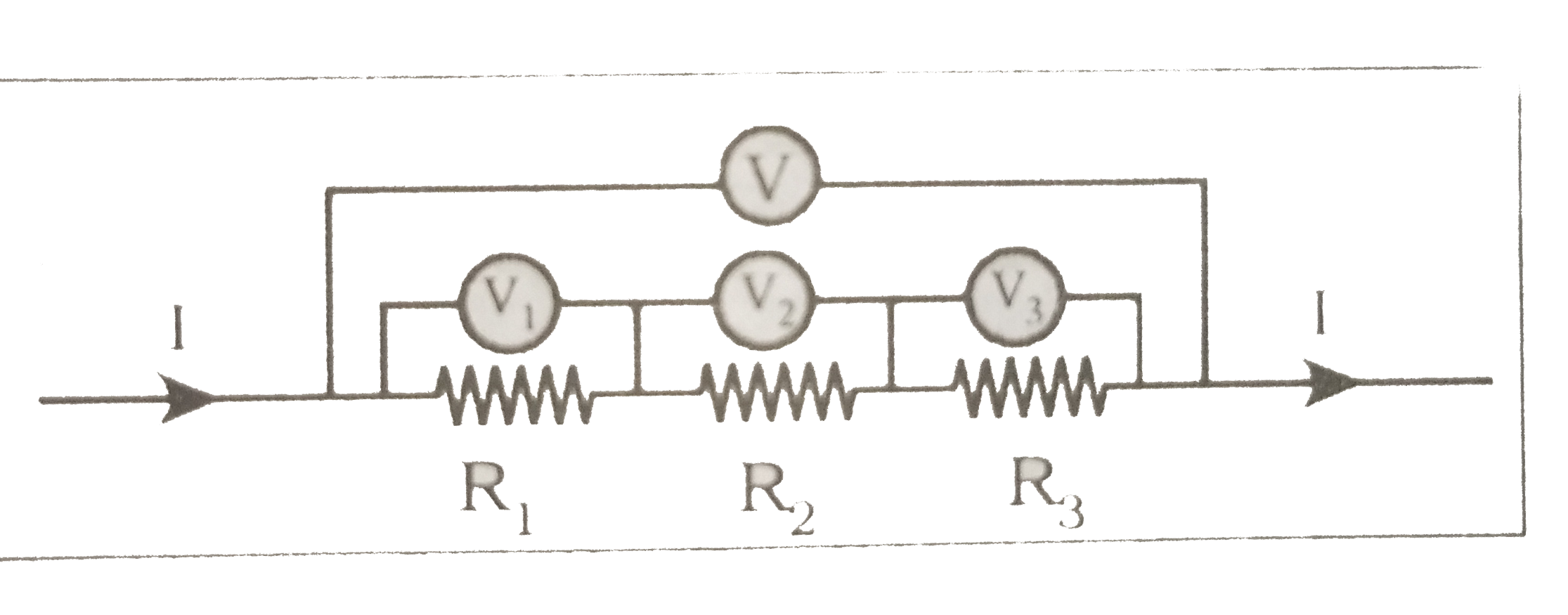
In series connection of resistors there is only one path for the flow of current in the circuit. Hence, the current in the circuit is equal to I.
According to Ohm's law,
∴V1=IR:V2=IR2andV3=IR3.
⇒ Let R be the equivalent resistance of the combination of resistors in series.
Also V=IReq
V=V1+V2+V3
IReq=IR1+IR2+IR3
rArrcancel(I)R_(eq)=cancel(I)(R_(1)+R_(2)+R_(3))
⇒Req=R1+R2+R3
∴ The sum of individual resistance is equal to their equivalent resistance when the resistors are connected in series.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - APPLICATION TO DAILY LIFE, CONCERN TO BIODIVERSITY37videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - FILL IN THE BLANKS8videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - SECTION - IV (4 Marks Questions)16videos
ELECTRIC CURRENT
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - CHEMICAL REACTIONS AND EQUATIONSEXERCISE - ESSENTIAL MATERIAL FOR EXAMINATION PURPOSE1videos
CHEMICAL REACTIONS AND EQUATIONS
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTROMAGNETISMEXERCISE - CREATIVE QUESTION FOR NEW MODEL EXAMINATION (SEC-4)30videos
ELECTROMAGNETISM
Similar Questions
Find an expression for the equivalent resistance of three resistors joined in series.
View SolutionDerive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.View Solution
Knowledge Check
- Question 1 - Select One
The equivalent resistance of resistors connected in series is always
AEqual to the mean of component resistorsBLess than the lowest of component resistorsCIn between the lowest and the highest of component resistorsDEqual to sum of component resistors - Question 2 - Select One
In an experiment to find the equivalent resistance of two resistors connected in series, a student uses the circuit shown :
This circuit will give :
 Acorrect reading for voltage V but incorrect reading for current IBcorrect reading for current I but incorrect reading for voltage (V)Ccorrect readings for both voltage V and current IDIncorrect readings for both current I and voltage V
Acorrect reading for voltage V but incorrect reading for current IBcorrect reading for current I but incorrect reading for voltage (V)Ccorrect readings for both voltage V and current IDIncorrect readings for both current I and voltage V - Question 3 - Select One
Choose the appropriate set of apparatus for performing the experiment to determine the equivalent resistance of two resistors when connected in series :
AVoltmeter, Ammeter, Two resistors, Key, BatteryBAmmeter, Two resistors, Key, Connecting wires, Rheostat, BatteryCKey, Rheostat, Voltmeter, Two resistors, Battery, Connecting wiresDBattery, Ammeter, Connecting wires, Rheostat Voltmeter, Two resistors, Key
The equivalent resistance of three equal resistances connected in series is 27Ω. There equivalent resistance when connected in parallel is
View SolutionTwo resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
View SolutionTwo resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
View SolutionThe resistors of resistances R1=100±3 ohm and R2=200±4ohm are connected in series. The equivalent resistance of the series combination is
View SolutionThe equivalent resistance of n identical resistors connected in parallel is x. If the resistors are connected in series, the equivalent resistance would be
View Solution

