Define trajectory of a projectile and hence derive equation of motion of the projectile when projected at an angle θ with horizontal direction.

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for Define trajectory of a projectile and hence derive equation of motion of the projectile when projected at an angle theta with horizontal direction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11PHYSICSRECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A particle is projected from the top of a tower of height h with a speed u at an angle θ above the horizontal .
    T1=Time taken by the projectile to reach the height of tower again .
    T2=Time taken by the projectile to move at right angle to initial direction of motion .
    V1=Speed of the projectile when it moves at an angle θ/2 with the horizontal .
    V2=Speed with projectile strikes the ground .
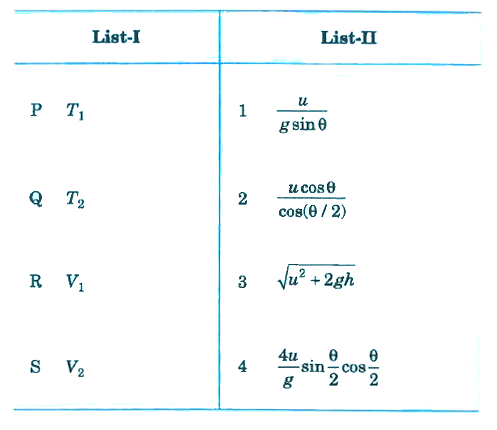    . ocr_image

    APQRS4123
    BPQRS1234
    CPQRS2413
    DPQRS2134

  • The question given below consist of an assertion and the reason . Use the following key to choose appropriate answer:
    Assertion: Range of projectile motion is same when particle is projected at an angle θ with the horizontal or at an angle (90∘−θ) with the horizontal .
    Reason : Range of projectile motion depended only on the angle of projection.

    AIf both assertion and reason are correct and reason is a correct explanation of the assertion
    BIf both assertion and reason are correct but reason is not the correct explanation of assertion .
    CIf assertion is correct but reason is incorrect .
    DIf both assertion and reason are incorrect .

  • The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is

    Asin1x
    Bcos−1x
    Csin−1(1/x)
    Dcos−1(1/x)