Density of a liquid varies with depth as h. A small ball of density is released from the free surface of the liquid. Then
the ball will execute SHM of amplitude
the mean position of the ball will be at a depth
the ball will sink to a maximum depth of
The ball sink to a maximum depth of
The correct Answer is:A, C, D
Step by step video, text & image solution for Density of a liquid varies with depth as rho=alphah. A small ball of density rho_(0) is released from the free surface of the liquid. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
(a). Discuss two situations in daily life where we apply the concept of pressure.
(b). A body of density ρ is dropped gently on the surface of a liquid of density ρ' (ρ' being less than ρ). Show That it will reach the bottom of the liquid after a time √2dρg(ρ−ρ'), where g is acceleration due to gravity and d is the depth of the liquid.
View SolutionA liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
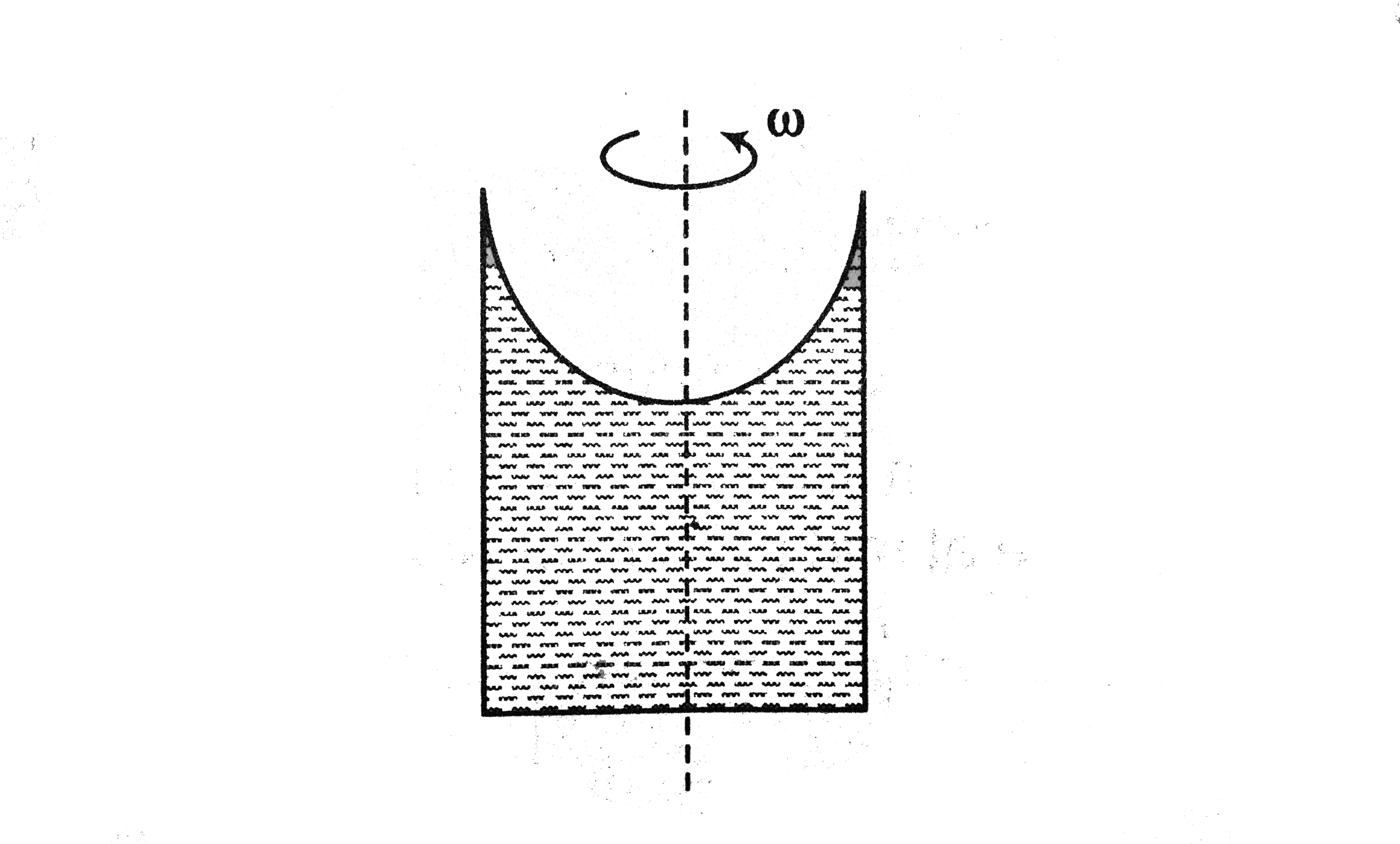 .
.
View Solution
Knowledge Check
The density ρ of a liquid varies with depth h from the free surface as ρ=kh. A small body of density ρ1 is released from the surface of liquid. The body will
Acome to a momentary rest at a depth 2ρ1/k from the free surfaceBexecute S.H.M. about a point at a depth ρ1/k from the surfaceCexecute S.H.M. of amplitude ρ1/kDall of theseA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
Awith an increasing accelerationBwith a decreasing accelerationCwith a constant accelerationDwith zero accelerationA triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
A12AρghB13AρghC16AρghD23Aρgh
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
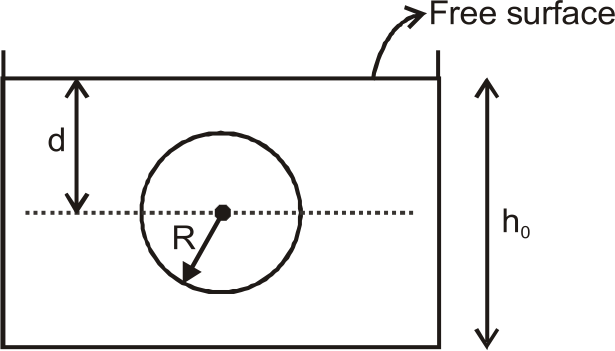
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA small ball of density 4ρ0 is released from rest just below the surface of a liquid. The density of liquid increases with depth as ρ=ρ0(1+ay) where a=2m−1 is a constant. Find the time period of its oscillation. (Neglect the viscosity effects).
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View Solution
