A liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
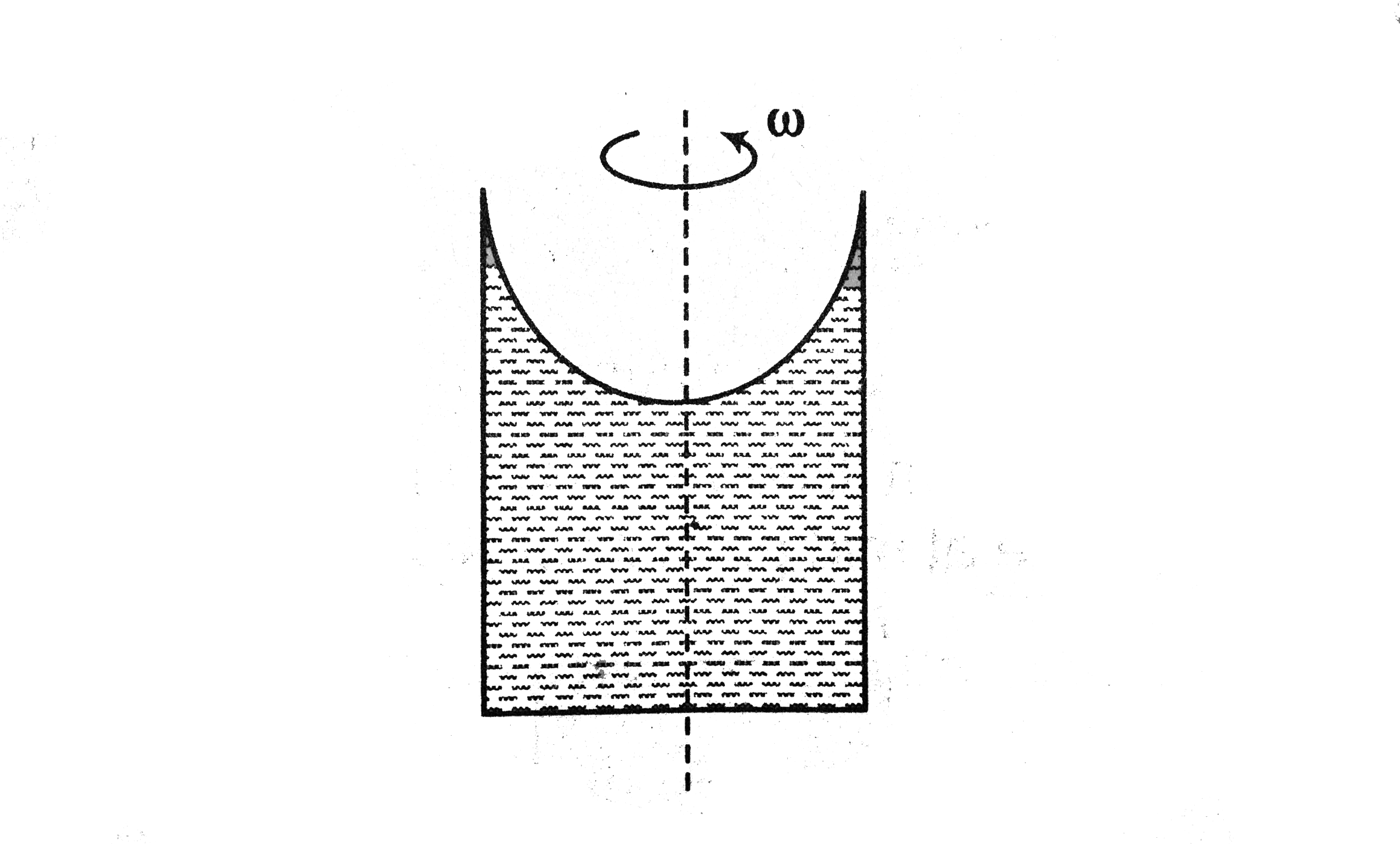 .
.
The correct Answer is:A
In the figure shown, suppose the coordinates of point M are (x,y) with respect to the coordinates axes.

Then, MN=y,NQ=x
Points M and Q are open to atmosphere.
∴pM=pQ=atmosphric pressure p_(0)<br>Now,pM−pN=−ρgy
⇒p0−pN=−ρgy ...(i)
pN−pQ=ρω2x22
∴pN−p0=ρω2x22...(ii)
Adding Eqs. (i) and (ii), we have
0=−ρgy+ρω2x22
y=ω2x22g
This is required equation of free surface of the liquid and we can see that this is an equation of a parabola.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
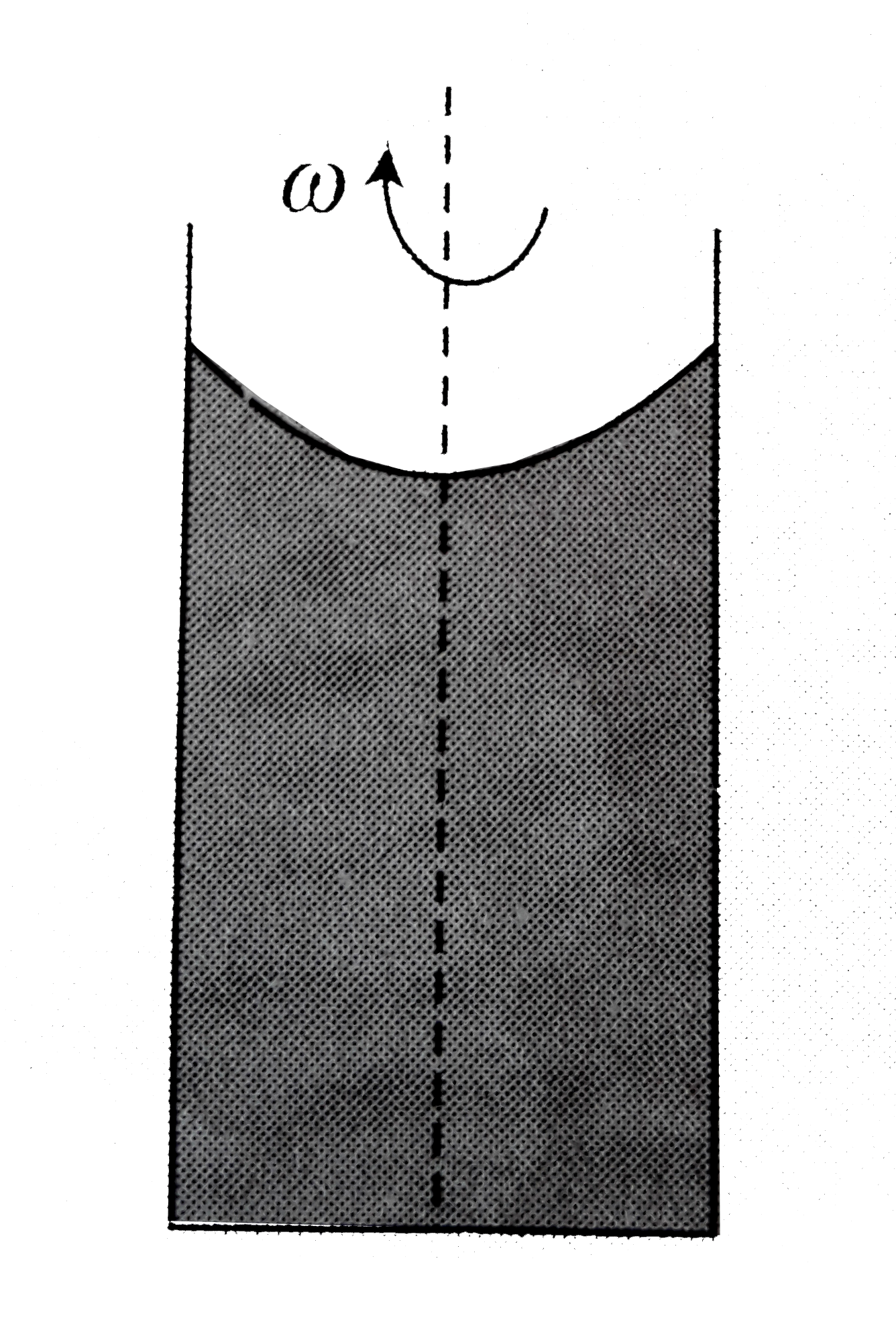 .View Solution
.View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
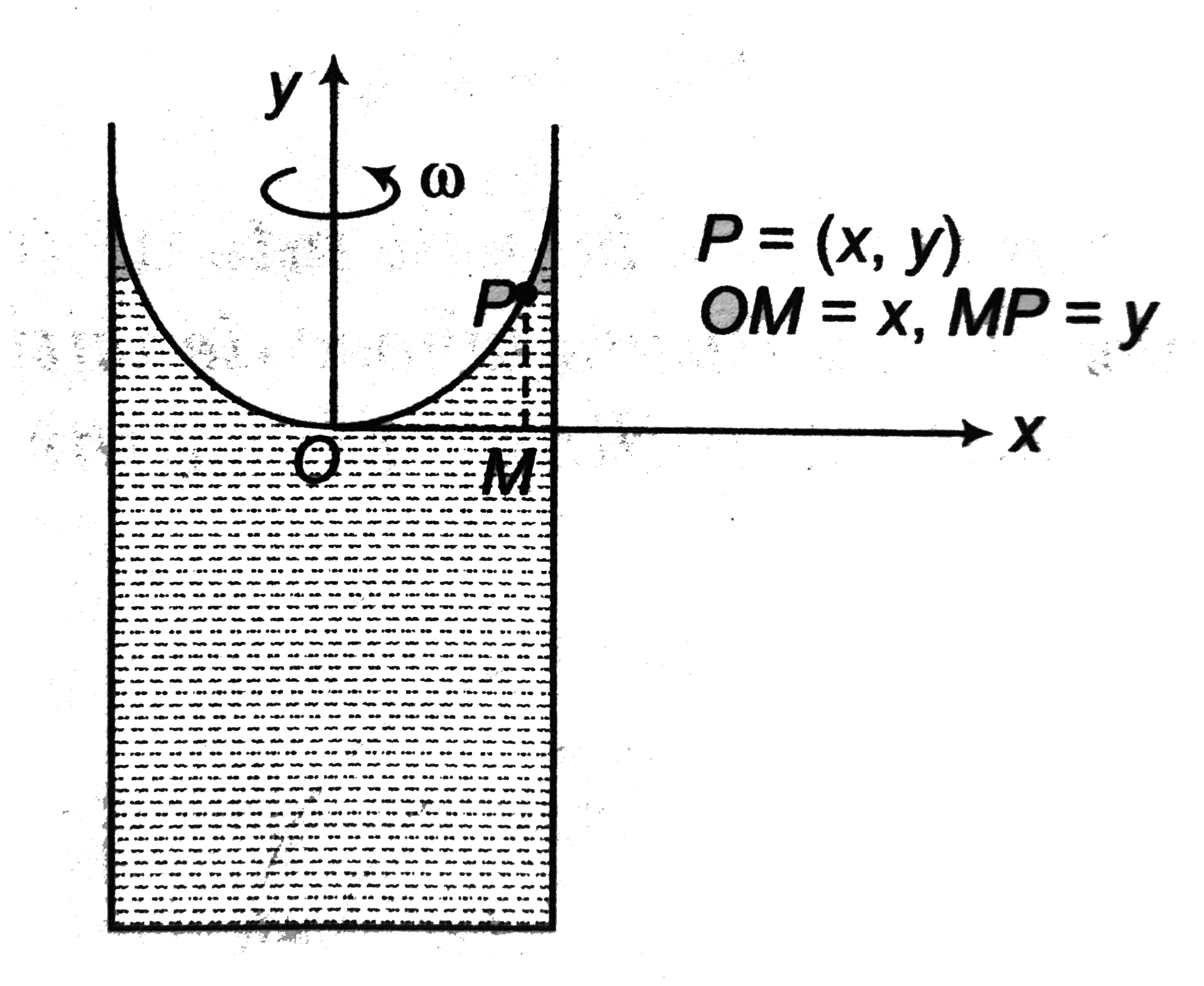 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
AparabolaBellipticalCcircularDspherical - Question 2 - Select One
A body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move
 Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of these
Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of these - Question 3 - Select One
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDg

A liquid of density ρ is rotated by an angular speed ω as shown in figure, Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
 View Solution
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View Solution

