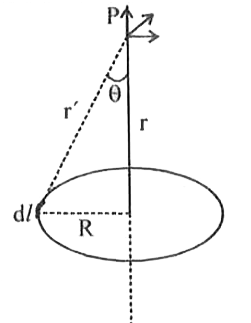
Derive an expression for field intensity due to a uniformly charged ring at a point on the axis. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

A ring of radius R is charged uniformly with linear density $λ = \frac{d q}{d l}$ . Consider a small element of length dl. The field intensity at the axial point P is $d E = \frac{1}{4 π ε_{0}} \frac{d q}{r^{2}}$ . This can be resolved into $d E sin θ$ - the perpendicular component and $d E cos θ -$ the parallel component. The perpendicular component gets cancelled by symmetry. The total field is $E = \int d E cos θ = \int \frac{d q}{4 π ε_{0} r^{.2}} cos θ = \int \frac{λ . d l}{4 π ε_{0} r^{.2}} cos θ$
The quantities r., $cos θ and λ$ are constants, as we look hte coil from P. Hence total field is
$E = \frac{λ cos θ}{4 π ε_{0} r^{.2}} \int d l = \frac{λ . cos θ}{4 π ε_{0} r^{.2}} \times 2 π R$
But $2 π R λ = total charge , q$
Hence $E = \frac{q}{4 π ε_{0} r^{.2}} cos θ = \frac{q}{4 π ε_{0}} \frac{1}{r^{.2}} \times \frac{r}{r .} = \frac{q r}{4 π ε_{0} r^{.3}} = \frac{q r}{4 π ε_{0} {(R^{2} + r^{2})}^{\frac{2}{3}}}$
When $R < < r, E = \frac{q}{4 π ε_{0} r^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

NEW JOYTHI PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Evaluation Questions And Answers

Home
Ask Doubt
Profile