Derive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart law. Solution in Telugu
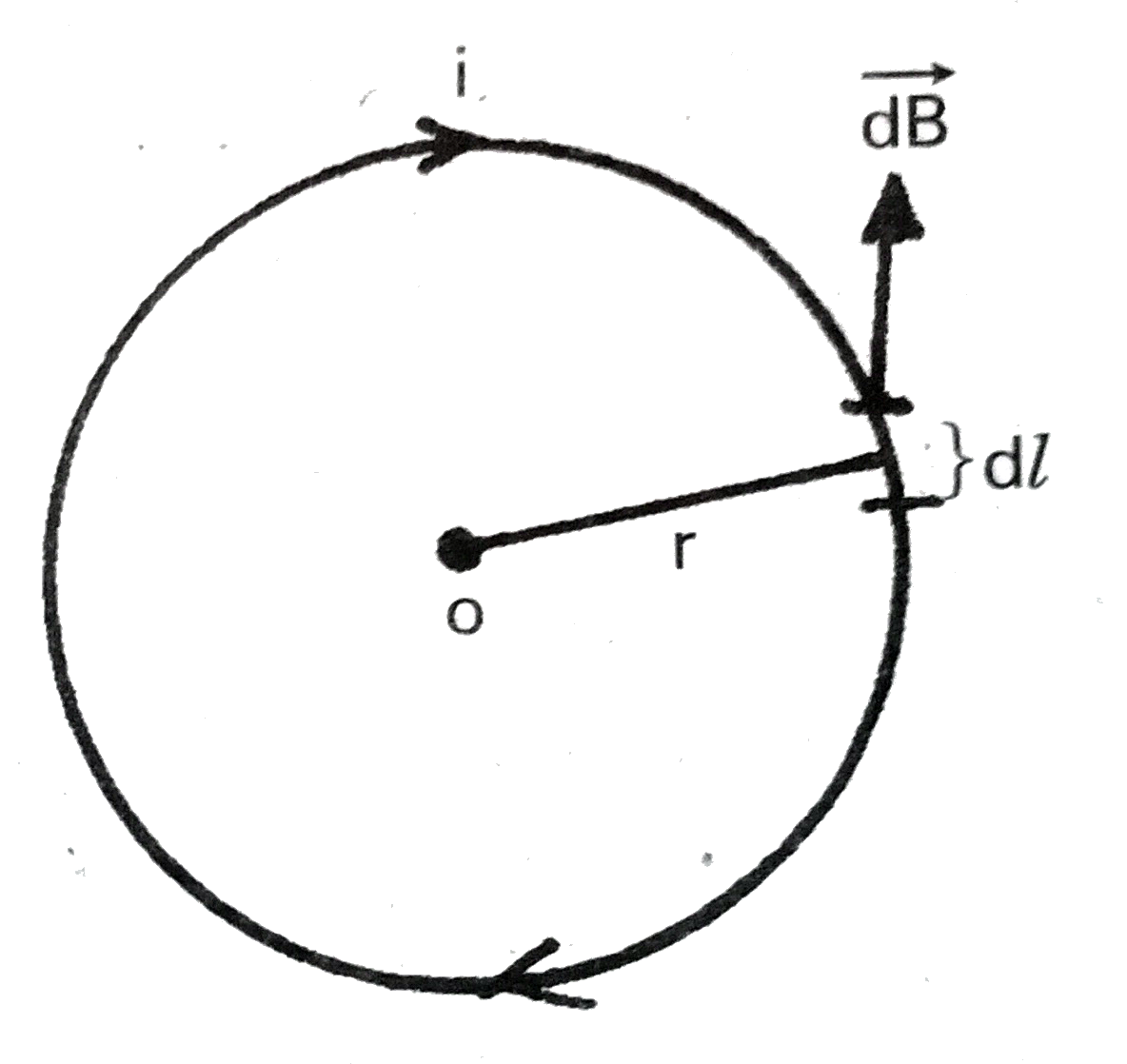
Consider a circular coil of radius r and carry a current i. Consider a small element 'dl'. Let O is the centre of the coil. By using Biot- Savart's law
dB=μ04π.Idlsinθr2
Here angle →dland→r is 90∘(i.e.θ=90∘)
dB=μ04πidlr2→(1)
As the field due to all elements of the circular loop have the same direction.
The resultant magnetic field can be obtained by integrating equation (1)
∫dB=∫μ04π.idlr2
B=μ0i4πr2∫dl ∵(∫dl=2πr)
=μ0i4πr2×2πr
B=μ0i2r
If the circular coil has n turns.
B=μ0ni2r
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISHMBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - MOVING CHARGES AND MAGNETISHMEXERCISE - LONG ANSWER QUESTIONS
5 Videos
- MOVING CHARGES AND MAGNETISHMBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - MOVING CHARGES AND MAGNETISHMEXERCISE - DAM SURE LAQ
2 Videos
- MOVING CHARGES AND MAGNETISHMBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - MOVING CHARGES AND MAGNETISHMEXERCISE - VERY SHORT ANSWER QUESTIONS
15 Videos
- MAGNETISM AND MATTERBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - MAGNETISM AND MATTEREXERCISE - Additional Exercises
19 Videos
- NUCLEIBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - NUCLEIEXERCISE - DAM SURE (VSAQ)
1 Videos
Similar Questions
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current. Carrying conductors.
View SolutionHow can a galvanometer be converted to an ammeter ? Why is the parallel resistance smaller that the galvanometer resistance ? A moving coil galvanometer can measure a current of 10−6 A. What is the resistance of the shunt required if it is to measure 1A ?
View SolutionWhat is the importance of Oersted's experiment ?
View SolutionWhy does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
View SolutionThe half life of .58Co is 72 days. Calculate its average life.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
View SolutionDetermine the magnetic induction at the centre of a circular coil of radius r carrying a current I with the help of the Biot-Savart law.
View SolutionDetermine the magnetic field in the following cases applying Biot-Savart law :
at the centre of a current carrying circular loop.
View SolutionState the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View SolutionUsing Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionState Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View Solution
