State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?

Video Solution

Text Solution

Verified by Experts

(a) Biot -Savart Law : "Magnetic fields acting at a particular point due to current carrying element is proportional to the division pf cross product of the current element and position vector of point where the field is to be calculated from the current element to the cube of the distance between current element and the point where the field is to be calculated."
$d B = \frac{μ . j dl sin θ}{4 π . r^{2}}$

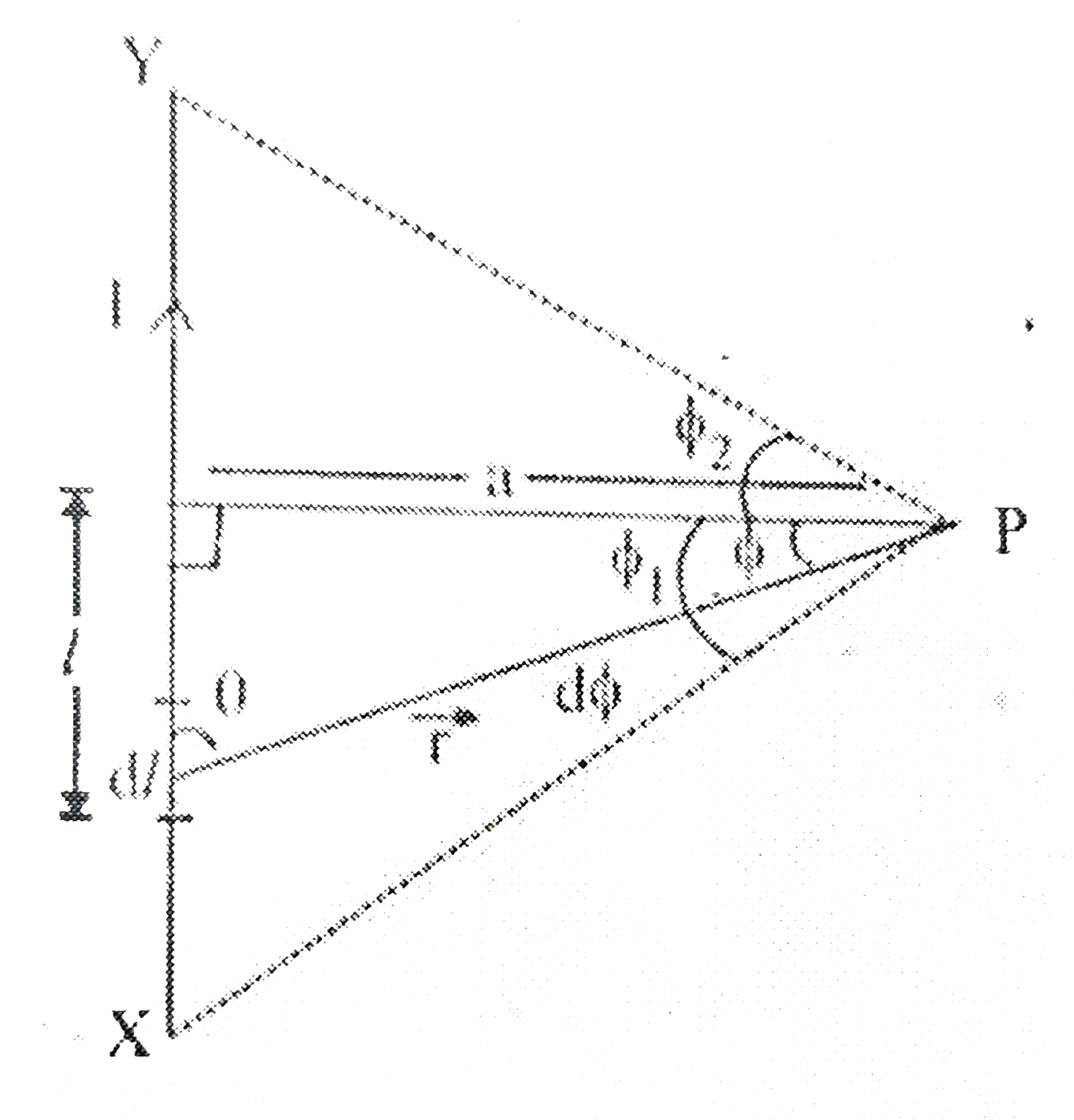
(b) Magnetic field due to a straight conductor carrying current : A long straight conductor XY carrying current I from X to Y. Let P be a point at a perpendicular distance 'a' from the conductor. Such that PC = a.
Consider a small current element of length dl of the conductor. Let $\to r$ be the position vector of Pw.r.t current element and $θ$ be the angle between $\to d l and \to r$ .
According to Biot-Savart's Law, the magnetic field at point p due to current element dl is
$d B = \frac{μ}{4 π} \frac{I d l sin θ}{r^{2}}$
In rt $Δ P O C, θ + ϕ = 90^{\circ}$
$θ = 90 - ϕ$
$sin θ = sin (90^{\circ} - ϕ) = cos ϕ$
$cos ϕ = \frac{a}{r} \Rightarrow r = \frac{a}{cos ϕ} = a sec ϕ$ .
Also $tan ϕ = \frac{l}{α} \Rightarrow l = a tan ϕ$
Now $d l = α {sec}^{2} ϕ d ϕ$
Thus,
$d B = \frac{μ_{o}}{4 π} \frac{I a {sec}^{2} ϕ d ϕ . cos ϕ}{a^{2} {sec}^{2} ϕ} \Rightarrow d B = \frac{μ_{o}}{4 π} \frac{1}{a} cos ϕ d ϕ$
According to right hand rule, the direction of $- \to d B$ is perpendicular to the plane of paper and directed inwards.
Since all the current elements of the conductor, produce magnetic field in the same direction. Therefore, total magnetic field at point P through whole conductor is
$B = ϕ_{2} \int - ϕ_{i} d B = ϕ_{2} \int - ϕ_{i} \frac{μ_{0}}{4 π} \frac{I}{a} cos ϕ d ϕ \Rightarrow B = \frac{μ_{o}}{4 π} \frac{1}{a} ϕ_{2} \int - ϕ_{1} cos ϕ d ϕ$
$B = \frac{μ_{o}}{4 π} \frac{1}{a} {[{sin ϕ}_{2}]}_{2}^{ϕ_{2}} \Rightarrow B = \frac{μ_{0}}{4 π} \frac{I}{a} [{sin ϕ}_{2} - sin (- ϕ_{1})]$
$B = \frac{μ_{o}}{4 π} \frac{I}{a} [{sin ϕ}_{2} + {sin ϕ}_{1}]$
For infinily long conductor, $ϕ_{1} = ϕ_{2} = \frac{π}{2}$
$B = \frac{μ_{0}}{4 π} \frac{I}{a} [sin . \frac{π}{2} + sin . \frac{π}{2}] \Rightarrow B = \frac{μ_{0}}{4 π} \frac{2 I}{a} \Rightarrow B = \frac{μ_{0}}{2 π} \frac{I}{a}$
(c) One face of current loop behaves as a south pole and other face as north pole. Therefore, the loop behaves as a magnetic dipole.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

XII BOARD PREVIOUS YEAR PAPER ENGLISH-XII BOARDS-PHYSICS (Theory) [SET -I]

Home
Ask Doubt
Profile