Derive th lens maker's formula.Solution in Kannada

Video Solution

Text Solution

Verified by Experts

Lens maker.s formula

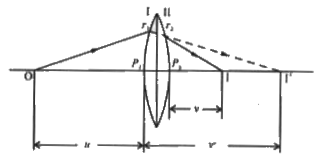
Let $r_{1} and r_{2}$ be the radii of curvature of the thin lens.
Let O be the point object at a distance u from the pole of the first curved surface of the lens. Real image is formed at I., at a distance v. from the pole $P_{1}$ . This image is formed in the denser medium.
We know that from the refraction formula.
$\frac{n_{1}}{- u} + \frac{n_{2}}{v} = \frac{n_{2} - n_{1}}{r}$
i.e., $\frac{n_{1}}{- u} + \frac{n_{2}}{v .} = \frac{n_{2} - n_{1}}{r_{1}}$ .......(1)
where $n_{1}$ is the refractive index of rarer medium and $n_{2}$ that of the denser medium $(n_{2} > n_{1})$ . For the second surface, real image at I. will serve as a virtual object and the distance is taken as -ve. The object space is the lens medium for refraction through the second curved surface. Final image is formed in air at I and at a distance of .v. from $P_{2}$
$\frac{n_{1}}{- u} + \frac{n_{2}}{v} = \frac{n_{2} - n_{1}}{r}$
i.e., $\frac{n_{2}}{- v .} + \frac{n_{1}}{v} = \frac{n_{2} - n_{1}}{- r_{2}}$ .......(2)
Adding (1) and (2) we get
$\frac{n_{1}}{- u} + \frac{n_{1}}{v} = (n_{2} - n_{1}) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$
or $\frac{1}{- u} + \frac{1}{v} = \frac{n_{2} - n_{1}}{n_{1}} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$ ..... (3)
when $u = \infty, v = f$
when $u = f, v = \infty$
$∴$ The term on the L.H.S. can be replaced by $\frac{1}{f}$ where f is the focal length of lens.
i.e., $\frac{1}{f} = (\frac{n_{2} - n_{1}}{n_{1}}) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$ ......(4)
Note: (1) Using the equation (4), it can be shown that
$_{1} n_{2} = 1 - [\frac{r_{1} r_{2}}{f (r_{1} - r_{2})}] {where,}_{1} n_{2} = \frac{n_{2}}{n_{1}}$ .
(2) For radius of curvature the letter .R. may be used.

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

SUBHASH PUBLICATION-RAY OPTICS AND OPTICAL INSTRUMENTS-FIVE MARKS QUESTIONS WITH ANSWERS

Home
Ask Doubt
Profile