Derive the equation of motion, range and maximum height reached by the particle thrown at an oblique angle $θ$ with respect to the horizontal direction. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

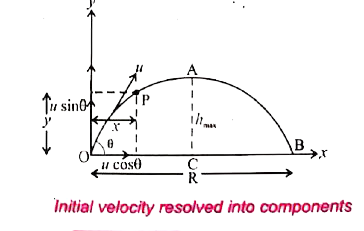
Let us consider an object thrown with initial velocity $\to u$ an angle $θ$ with the horizontal as in figure
$\to u = u_{z} ˆ i + u_{y} ˆ j$
The horizontal component of velocity $u_{x} = u cos θ$ . The vertical component of velocity $u_{y} = u sin θ$ .
Since the acceleration due to gravity is in the direction opposite to the direction of vertical component $u_{y}$ this component will gradually reduce to zero at the maximum height of the projectile. At this maximum height, the same gravitational force will push the projectile to move downward . It falls to the ground. there isno acceleration along the x direction throughout the motion. Hence, the horizontal component of the velocity $(u_{x} = u cos θ)$ remains the same till the object reaches the ground .
Hence after the time t , the velocity along horizontal motion $v_{x} = u_{x} + a_{x} t$ [ $∵ u_{x} = u cos θ$ ]
The horizontal distance travelled by projectile in time t is $s_{x} = u_{x} t + \frac{1}{2} a_{x} t^{2}$
Here, $s_{x} = x, u_{x} = u cos θ, a_{x} = 0$
Thus , x $= u cos θ t or t = \frac{x}{u cos θ} . . . (1)$
For the vertical motion $v_{y} = u_{y} + a_{y} t$
Here $u_{y} = u sin θ, a_{y} = - g$ (acceleration due to gravity acts opposite to the motion) . Thus
$v_{y} = u sin θ - g t . . . (2)$
the vertical distance travelled by the projectile in the same time t is
$s_{y} = u_{y} t + \frac{1}{2} a_{y} t^{2}$
Here , $s_{y} = y, u_{y} = u sin θ, a_{x} = - g .$ Then
$y = u sin θ t - \frac{1}{2} g t^{2} . . . (3)$
Substitute the value of t from equation (1) in equation (3) , we have

$y = u sin θ \frac{x}{u cos θ} - \frac{1}{2} \frac{g (x^{2})}{u^{2} {cos}^{2} θ}$
$y = x tan θ - \frac{1}{2} \frac{g (x^{2})}{u^{2} {cos}^{2} θ} . . . (4)$
Thus the path followed by the projectile is an inverted parabola.
Maximum height $(h_{max})$ :
The maximum vertical distance travelled by the projectile during its journey is called maximum height
For the vertical part of the motion,
$v_{y}^{2} = u_{y}^{2} + 2 a_{y^{s}}^{s}$
Here, $u_{y} = u sin θ, a = - g, s = h_{max}$ , and at t he maximum height $v_{y} = 0$
$∴ (0) = u^{2} {sin}^{2} θ = 2 g h_{max}$
or $h_{max} = \frac{u^{2} {sin}^{2} θ}{2 g}$
Horinontal range (R) : The maximum horizontal distance between the point of projection and the point on the horizontal plane where the projectile hits the ground is called horizontal range (R) . It is found easily. Since the horizontal component of initial velocity remains the same.We can write $Range R = {\begin{matrix} Horizontal component of velocity \times time of flight \end{matrix}$
$= u cos θ \times T_{f}$
$R = u cos θ \times \frac{2 u sin θ}{g}$
$= \frac{2 u^{2} sin θ cos θ}{g}$
$\Rightarrow ∴ R = \frac{u^{2} sin 2 θ}{g}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

PREMIERS PUBLISHERS-KINEMATICS -Textbook questions & answers (III. Long answer questions).

Home
Ask Doubt
Profile