Derive the expression for magnetic field at a point on the axis of a circular current loop. Solution in Kannada
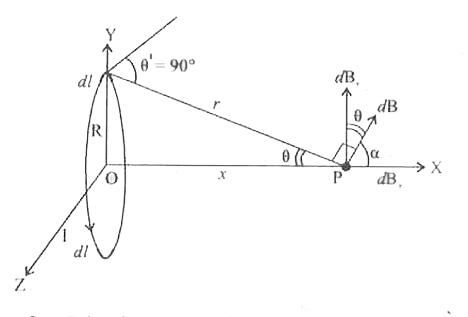
Let R be the radius of a current loop, carrying current I. Let R be a point on the axis of a conductor. Let dB be magnetic field at P, due to a current element .idl.
From the figure, θ+a=90∘, so that α=90∘–0 and cosα=cos(90∘–0)
sinθ=R2(R2+x2)12...(1)
Let dBx be the horizontal component of dB.
Applying Biot-Savart.s law ,
We write
d→B=(μ04π)I(d→l×→r)r3
i.e., dB=(μ04π)Irdlr3sinθ.
where θ.=90∘
i.e., dB=(μ04π)Irdlr3=(μ04π)Idlr2 ...(2)
Component of dB along the horizontal is
dBx=dBcosα
or dBx=dBsinθ
=(μ04π)Idlr2sinθ
By using (1) we write
dBx=(μ04π)Idlr2Rr=(μ04π)IdlR(R2+x2)32...(3)
or integrating
Bx=∫dBx=∫(μ04π)IR(R2+x2)32dl
i.e., Bx=(μ04π)IR(R2+x2)32dl
i.e., Bx=(μ04π)IR(R2+x2)32(2πR)
where ∫dl=2πR
or Bx=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ tesla
and →B=Bxˆi=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ˆi,
dBy=0
For a circular loop , and at the centre , x=0
→B=(μ04π)(2πIR)ˆi
For a circular conductor containing n turns ,
Bxˆi=(μ04π)2πnIR2(R2+x2)32ˆi
and at the centre ,
B0ˆi=(μ04π)(2πnIR)ˆi
Topper's Solved these Questions
Similar Questions
A spherical hollow conductor is charged to -250V. If the radius of the conductor is 0.15m, then calculate
(i) Charge on the conductor.
(ii) Electric files intensity on the surface
(iii) Electric field intensity at the centre.
(iv) Electric potential difference between A and B at distances of 0.20 m & 0.25m from the centre respectively.
View SolutionFor a short magnetic dipole of magnetic moment 0.5 Am2. Find the magnetic field at a point ( a) 1 m on the axis and from the cetre of the magnet ( dipole ) ( b) 1 m on the equatorial line from the centre ( c) at an angle of 60∘ w.r. to the line joining the point and the centre of the dipole at distance 1 m.
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
View SolutionDerive an expression for the magnetic field at a point on the axis of a current carrying circulat loop.
View SolutionUsing Biot-Svart's law, derive the expression for the magnetic field in vector form at a point on the axis of a circular current loop.
View SolutionDerive the expression for the magnetic field on the axis of a circular current loop , using Biot-Savart's law.
View SolutionUsing Biot Savart's law, derive the expression for the magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop .
View SolutionGive the expression for magnetic field at a point on the axis of a short magnetic dipole.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive an expresion for the magnetic field at any point on the axis of a circular current loop.
View SolutionUsing Biot Savart’s law derive an expression for the magnetic field due to a circular current carrying loop at any point on its axis.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View Solution
