Question

$\text{Derive}\frac{1}{Rp}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}.$(Resistors in parallel)

Explanation

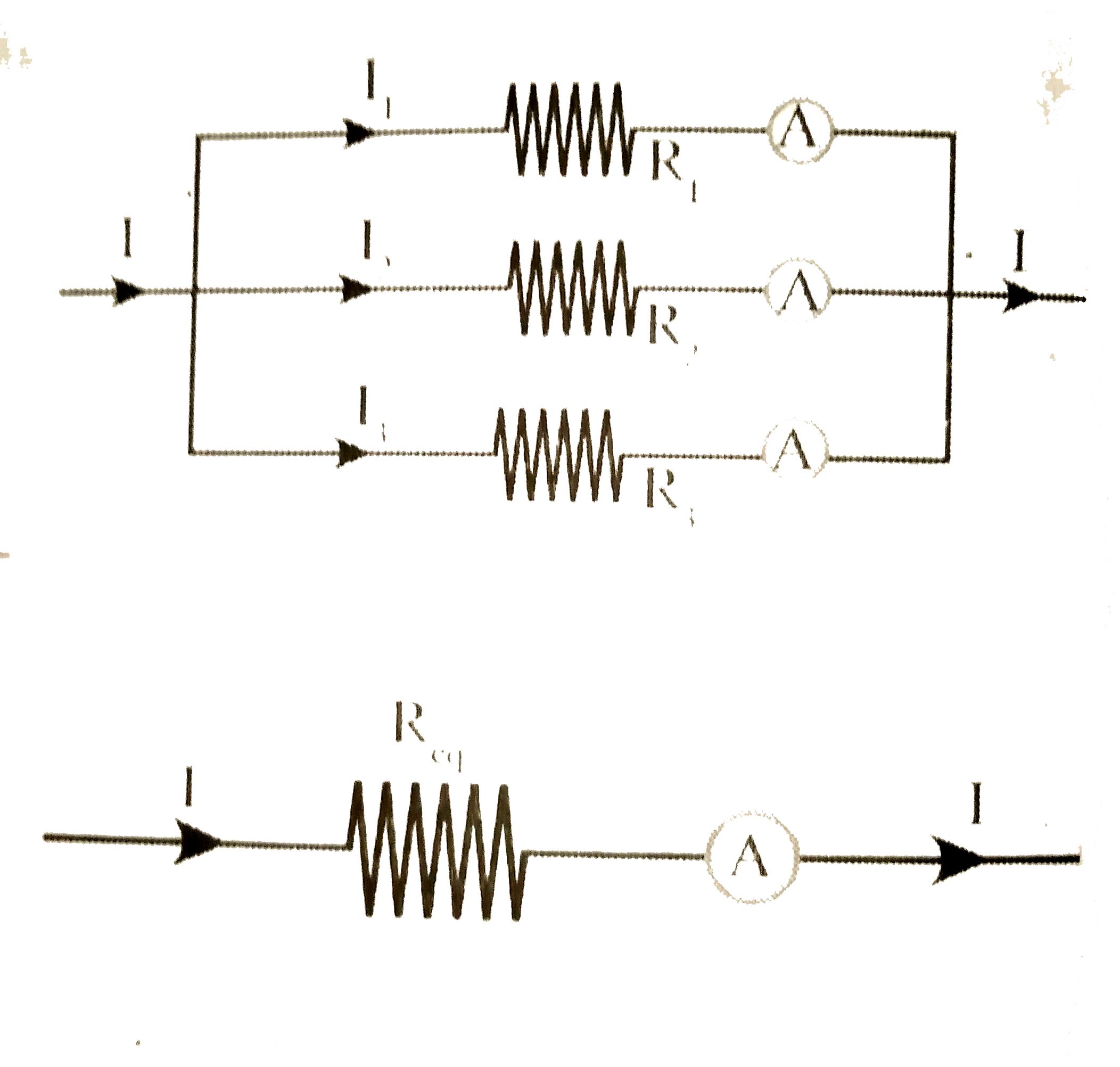
Parallel Connection : In Parallel connection of resistors there is same potential difference at the ends of the resistors. Hence the voltage in the circuit is equal to V.
Let `I_(1),I_(2)andI_(3)` be the currents flowing through `R_(1),R_(2)andR_(3)` resistors respectively.
Hence, we can write `I=I_(1)+I_(2)+I_(3).`
According to the Ohm's law.
`V_(1)=1_(1)R_(1),V_(2)=I_(2)R_(2),V_(3)=I_(3)R_(3)`
here,`V=V_(1)=V_(2)=V_(3)`
`thereforeV=I_(1)R_(1),V=I_(2)R_(2),V=I_(3)R_(3)`
`rArrI_(1)=(V)/(R_(1)),I_(2)=(V)/(R_(2))andI_(3)=(V)/(R_(3))`
`thereforeI=I_(1)+I_(2)+L_(3)`
`rArr(V)/(R_(eq))=(V)/(R_(1))+(V)/(R_(2))+(V)/(R_(3))`
`rArrcancel(V)xx(1)/(R_(eq))=cancel(V)[(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))]`
`rArr(1)/(R_(eq))=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))(" here " R_(eq)" is the equivalent resistance ")`
`therefore` The equivalent resistance of a parallel combination is less than the resistance of each of the resistors.