Determine the period of small longitudinal oscillations of a body with mass m in the system shown in figure. The stiffness values of the springs are x1 and x2. The friction and the masses of the springs are negligible.
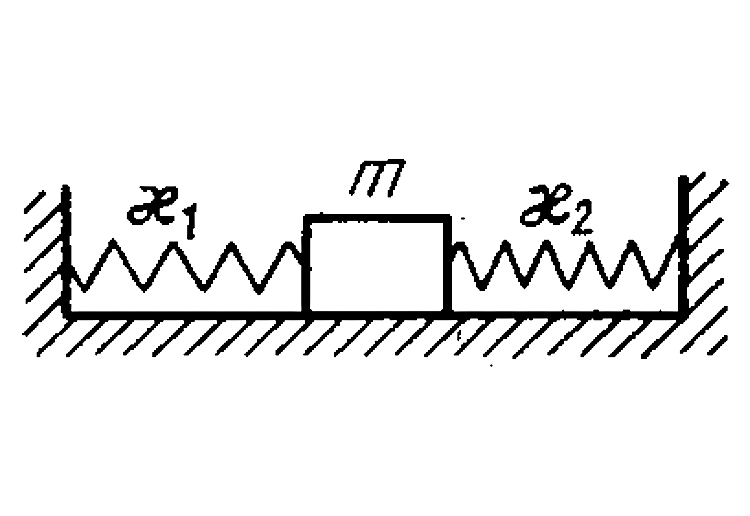
The net unbalanced force on the block m when it is at a small horiozontal distance x from the equilibrium position becomes (k1+k2)x
From Fx=mwx for the block :
−(k1+k2)x=m..x
Thus..x=−(k1+k2m)x
Hence the sought time period T=2π√mk1+k2
Alternate : Let us set the block m in motion to perform small oscillation . Let us locate the block when it is at a distance x from its equilibrium position.
As the spring force is restoring conservative force and deformation of both the springs are same, so from the conservation of mechanical energy of the spring − block system : 12m(dxdt)2+12k1x2+12k2x2= Constant
Differentiating with respect to time
12m2..x..x+12(k1+k2)2x.x=0
..x=−(k1+k2)mx
Hence the sought time period T=2π√mk1+k2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
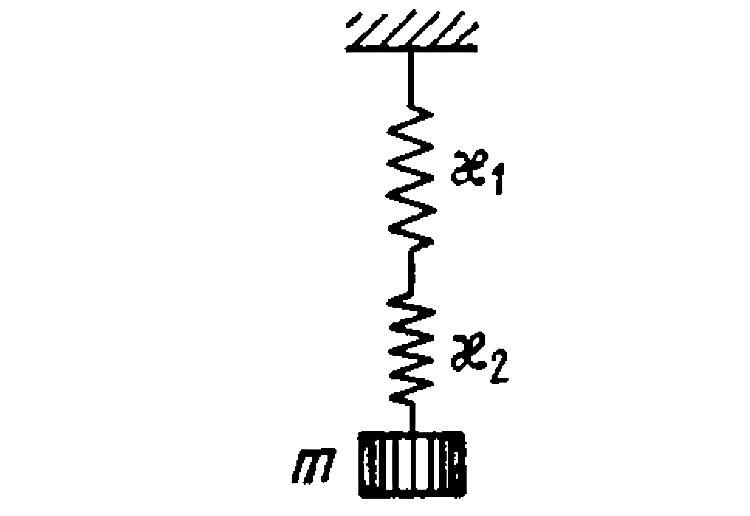
Find the period of small vertical oscillations of a body with mass m in the system illustrated in figure. The stiffness values of the springs are x1 and x2, their masses are negligible.
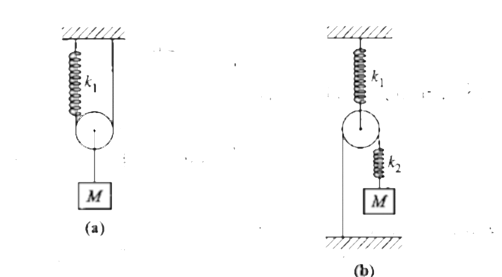
View SolutionFind the stretch in the springs shown in figure-2.112. The respective data are given in the figure. The friction and masses in pulleys are negligible.
View Solution
Knowledge Check
The frequency of vertical oscillations of the three spring-mass system, shown in figure, is
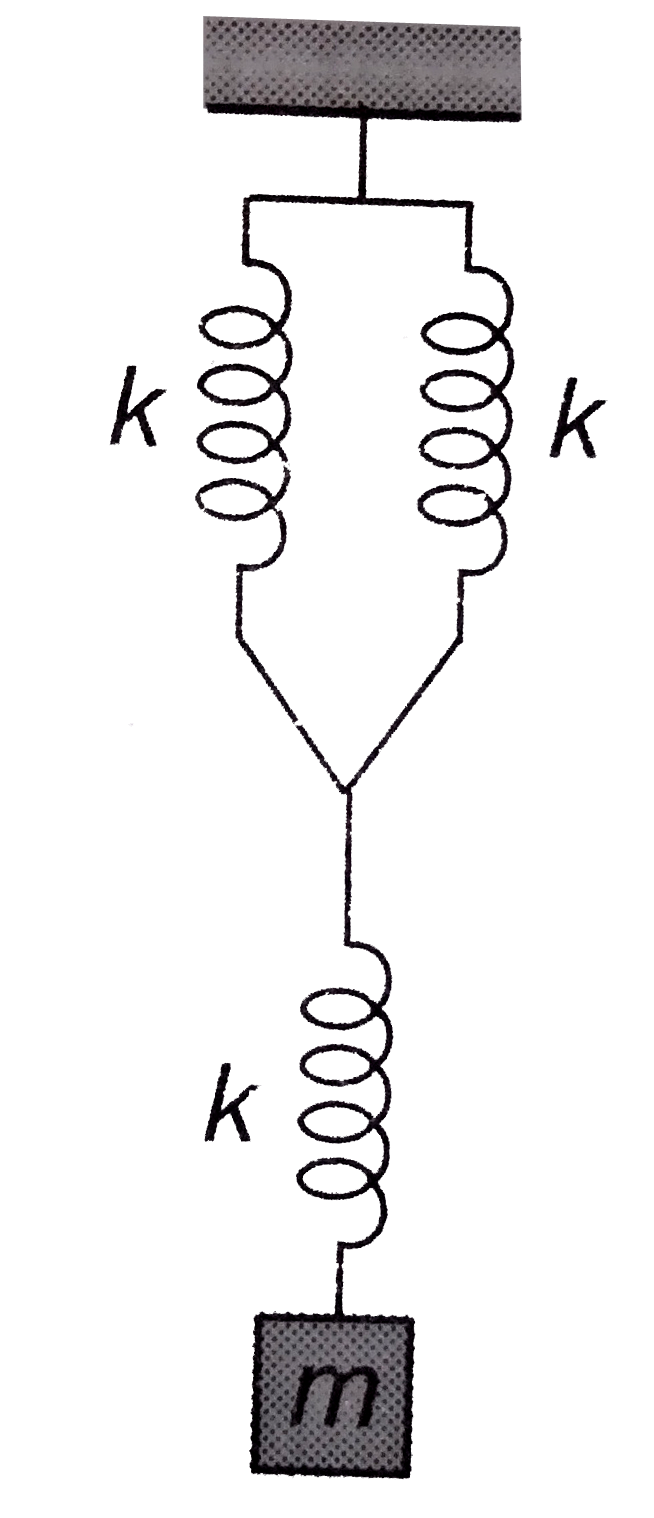 A12π√3k2mB12π√2k3mC12π√2kmD12π√k3m
A12π√3k2mB12π√2k3mC12π√2kmD12π√k3mCalculate the period of oscillations of block of mass m attached with a set of springs as shown
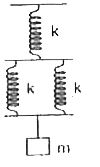 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmThe ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
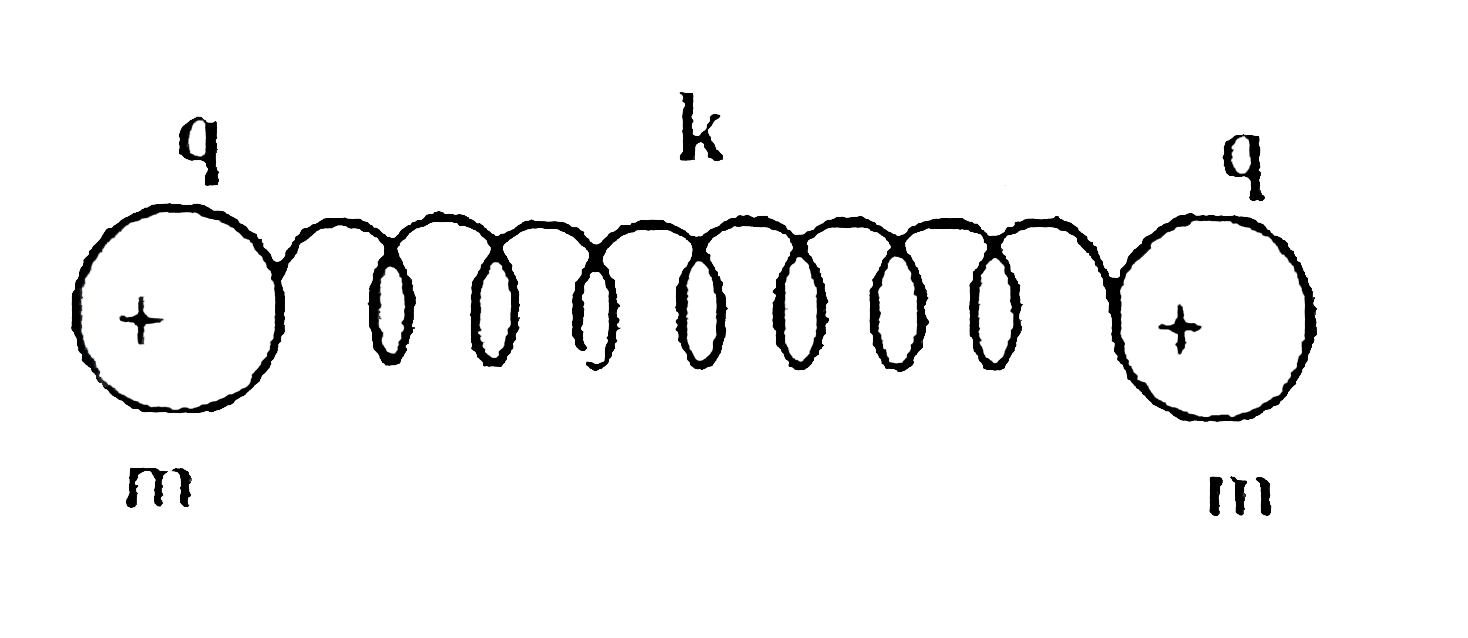 A≥1B>1C≤1D=1
A≥1B>1C≤1D=1
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
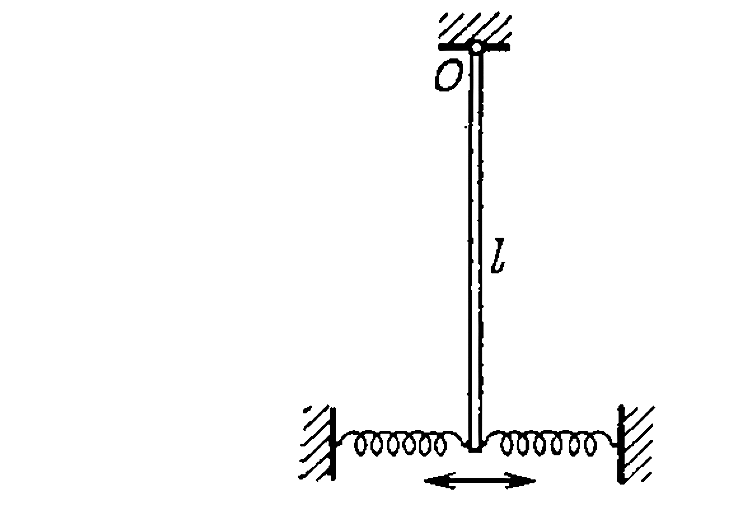
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
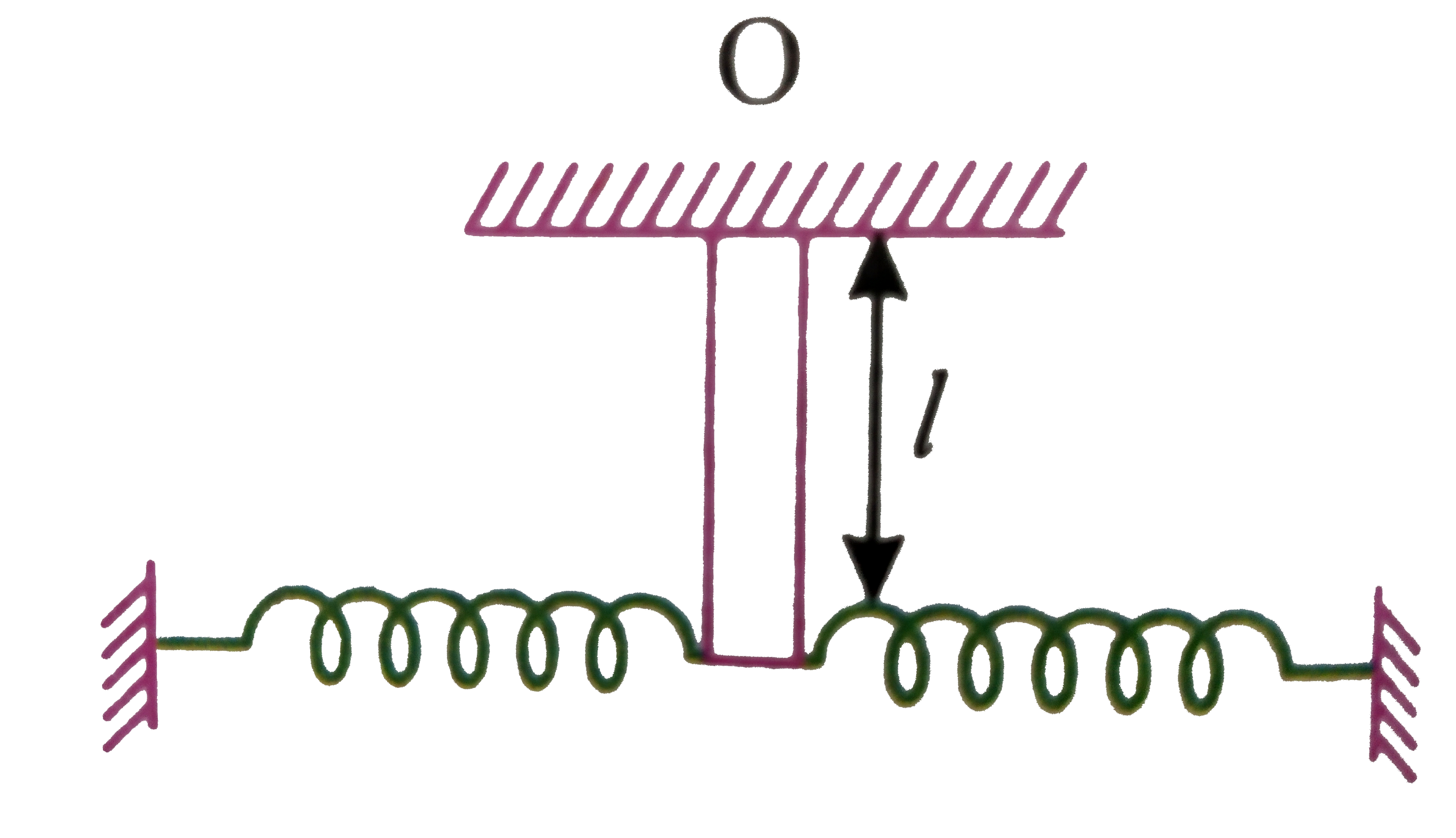
View Solution
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .
View SolutionThe period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
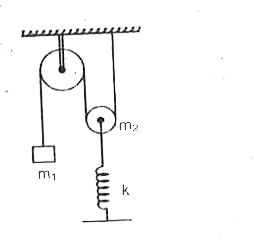
View Solution
