Determine the period of small oscillations of a mathematical pendulum, that is a ball suspended by a thread l=20cm in length, if it is located in a liquuid whose density is η=3.0 times less than that of the ball. The resistance of the liquid is to be neglected.
Let us depict the forces acting on the osciallating ball at an arbitraty angular position θ (figure), relative to equilibrium position where FB is the force of buoyancy. For the ball from the equation :
NZ=IβZ, (where we have taken the positive sense of Z axis in the direction of angular velocity i.e.,θ of the ball and passes through the point of suspension of the pendulum O), we get :
−mglsinθ+FBsinθ=ml2..θ...(1)
Using m=43πr3σ,FB=43πr3ρ andsinθ≅θ for small θ, for Eqn (1) , we get :
..θ=−gl(1−ρσ)θ
Thus the sought time period
T=2π1√gl(1−ρσ)=2α
⎷l/g1−1η
Hence t=2√ηlg(η−1)=1.1s

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A solid cube of sides 2 cm each is suspended by a thread and completely immersed in a liquid of density 0.85×103 kg/m3. What will be the tension in the thread if relative density of solid is 5?
View SolutionFind the period of small oscillations of a mathematical pendulum of length l if its point of suspension O moves relative to the Earth's surface in an arbitrary directio with a constant acceleration w (figure). Calculate that period if l=21cm,w=g/2, and the angle between the vectors w and g equals beat=120∘.
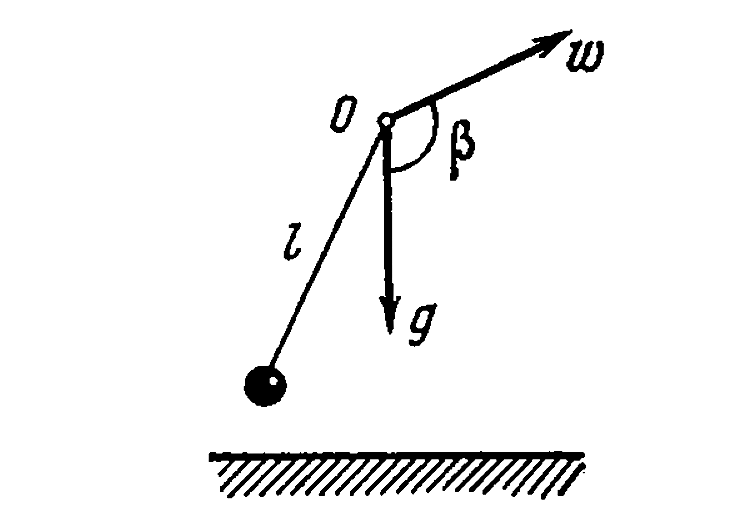
View Solution
Knowledge Check
The periodic time of a simple pendulum, oscillating in air is T. But if the bob of the simple pendulum is completely immersed in a nonviscous liquid, whose density is 120 th of the material of the bob, then its new period will be
ATB1920TC2019TD√2019TA simple pendulum oscillating in air has a time period of √3s. Now the bob of the pendulum is completely immersed in a non-viscous liquid whose density is equal to 14th that of the material of the bob. The new time period of simple pendulum will be
A√2sB√3sC2sD√72sA simple pendulum of length 4.9m is immersed in a liquid of density ρ=0.4kg/m3. Then the time period of pendulum is (density of bob =0.8kg/m3)
AπsB3πsC2πsDπ/2s
An external harmonic force F whose frequency can be varied, with amplitude maintained constant, acts in a vertical direction on a ball suspended by a weightless spring. The damping coefficient is η times less than the natural oscillation frequency ω0 of the ball. How much, in per cent, does the mean power (:P:) developed differ from the maximum mean power (:P:)max? Averaging is performed over one oscillation period.
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
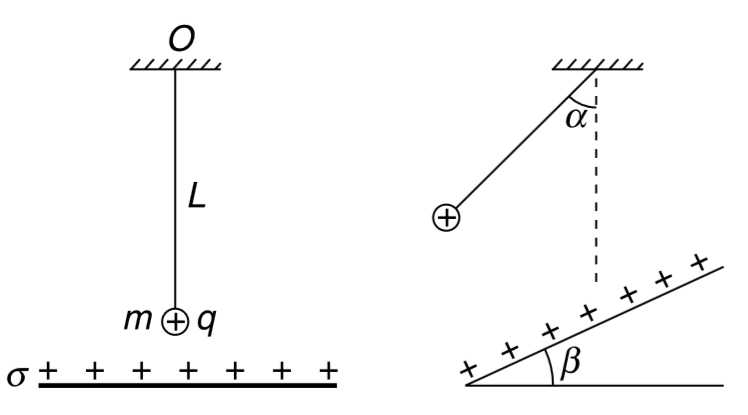
View SolutionThe time period of oscillation of a simple pendulum is given by T=2π√l/g
The length of the pendulum is measured as 1=10±0.1 cm and the time period as T=0.5±0.02s. Determine percentage error in te value of g.
View SolutionA uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
View SolutionThe time period of oscillation of a simple pendulum is given by T=2π√l/g
The length of the pendulum is measured as l=10±0.1 cm and the time period as T=0.5±0.02s. Determine percentage error in te value of g.
View Solution
