Diagrammatically show first two modes of vibrations in case of an open organ pipe and write the ratio of their frequencies
To solve the problem of showing the first two modes of vibrations in an open organ pipe and writing the ratio of their frequencies, we can follow these steps:
Step 1: Understand the Open Organ Pipe
An open organ pipe has both ends open, which means that at both ends, there are antinodes (points of maximum displacement). The length of the pipe (L) will determine the wavelengths of the sound waves produced.
Step 2: First Mode of Vibration (Fundamental Frequency)
- In the first mode of vibration (fundamental frequency), the length of the pipe corresponds to half a wavelength (λ/2).
- Therefore, we can write the relationship:
L=λ12
From this, we can express the wavelength:
λ1=2L
- The frequency (f) is related to the speed of sound (v) and the wavelength (λ) by the equation:
f=vλ
- Substituting λ with λ1:
f1=vλ1=v2L
- This frequency is known as the fundamental frequency (f0):
f0=v2L
Step 3: Second Mode of Vibration (First Overtone)
- In the second mode of vibration (first overtone), the length of the pipe corresponds to one full wavelength (λ).
- Therefore, we can write:
L=λ2
- The wavelength for the second mode is:
λ2=L
- The frequency for this mode is:
f2=vλ2=vL
- This frequency is twice the fundamental frequency:
f1=2f0=2(v2L)=vL
Step 4: Ratio of Frequencies
- Now, we can find the ratio of the frequencies of the first and second modes:
Ratio=f1f0=vLv2L=2LL=2
- Thus, the ratio of their frequencies is:
f0:f1=1:2
Step 5: Diagram
- Draw the first two modes of vibration:
- First Mode (Fundamental Frequency): A wave with one antinode at each end and one node in the middle.
- Second Mode (First Overtone): A wave with two antinodes and one node in the middle.
An open organ pipe has both ends open, which means that at both ends, there are antinodes (points of maximum displacement). The length of the pipe (L) will determine the wavelengths of the sound waves produced.
- In the first mode of vibration (fundamental frequency), the length of the pipe corresponds to half a wavelength (λ/2).
- Therefore, we can write the relationship:
L=λ12
From this, we can express the wavelength:
λ1=2L
- The frequency (f) is related to the speed of sound (v) and the wavelength (λ) by the equation:
f=vλ
- Substituting λ with λ1:
f1=vλ1=v2L
- This frequency is known as the fundamental frequency (f0):
f0=v2L
- In the second mode of vibration (first overtone), the length of the pipe corresponds to one full wavelength (λ).
- Therefore, we can write:
L=λ2
- The wavelength for the second mode is:
λ2=L
- The frequency for this mode is:
f2=vλ2=vL
- This frequency is twice the fundamental frequency:
f1=2f0=2(v2L)=vL
- Now, we can find the ratio of the frequencies of the first and second modes:
Ratio=f1f0=vLv2L=2LL=2
- Thus, the ratio of their frequencies is:
f0:f1=1:2
- Draw the first two modes of vibration:
- First Mode (Fundamental Frequency): A wave with one antinode at each end and one node in the middle.
- Second Mode (First Overtone): A wave with two antinodes and one node in the middle.
Similar Questions
Knowledge Check
- Question 1 - Select One
Modes of vibration in an open organ pipe are represented by –
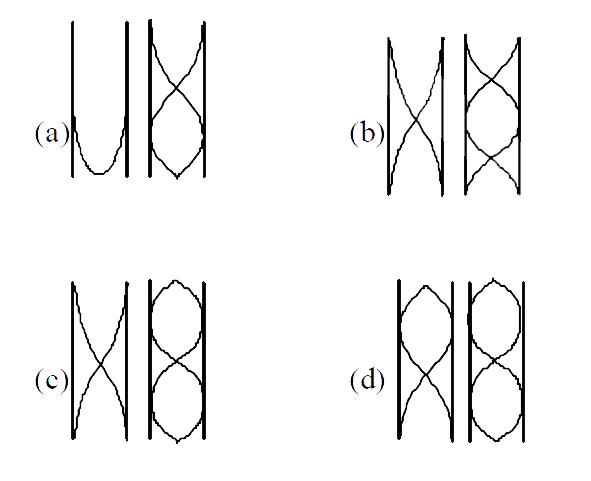 AaBbCcDd
AaBbCcDd - Question 2 - Select One
Modes of vibration in a closed organ pipe are represented by –
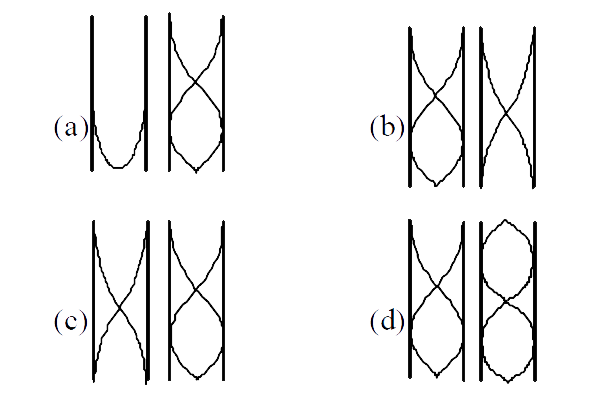 AaBbCcDd
AaBbCcDd - Question 3 - Select One
The frequency of vibration of open orgen pipe is
Av4lBv2l+1.2dCvlDv8l
Discuss various modes of vibration in open ends organ pipe. Also, show that the ratio of frequencies of different harmonics with first harmonic in open pipe is 1:2:3.
View SolutionDerive an expression for the nth mode of vibration in case of a closed end organ pipe. Hence give the value of v1:v2:v3.
View SolutionThe frequency of the first overtone of a closed organ pipe is same as that of first overtone of an open organ pipe. What is the ration of their lengths?
View SolutionThe frequency of open organ pipe is
View SolutionAssertion: The fundamental frequency of vibration of an open organ pipe remains same if the radius of the pipe is doubled.
Reason: Frequency of vibration of an open organ pipe is independent of the radius of pipe.View Solution

