Discuss the flow of a.c. through a pure resistor.
Step-by-Step Solution:
1. Understanding the Circuit:
We start with a simple circuit consisting of a pure resistor (R) connected to an alternating current (AC) source that provides an alternating electromotive force (EMF).
2. Expression for Alternating EMF:
The instantaneous value of the alternating EMF can be expressed as:
E(t)=E0sin(ωt)
where E0 is the peak EMF and ω is the angular frequency.
3. Ohm's Law Application:
According to Ohm's law, the relationship between the voltage (E), current (I), and resistance (R) is given by:
E=I⋅R
From this, we can express the current (I) flowing through the resistor as:
I=ER
4. Substituting the EMF Expression:
We substitute the expression for E(t) into the equation for current:
I(t)=E0sin(ωt)R
5. Defining Peak Current:
We can define the peak current I0 as:
I0=E0R
Therefore, the expression for instantaneous current becomes:
I(t)=I0sin(ωt)
6. Phase Relationship:
From the derived equations, we see that both the instantaneous EMF and the current are sinusoidal functions of time. Since they are both represented by sine functions with the same argument (ωt), it follows that the EMF and the current are in phase. This means that when the EMF reaches its maximum value, the current also reaches its maximum value simultaneously.
7. Graphical Representation:
This relationship can be represented graphically, where both the EMF (E) and the current (I) waveforms will have the same shape and peak at the same time.
Conclusion:
In a pure resistor, the alternating current is directly proportional to the alternating EMF, and both quantities are in phase with each other. This means that there is no phase difference between the voltage across the resistor and the current flowing through it.
---
We start with a simple circuit consisting of a pure resistor (R) connected to an alternating current (AC) source that provides an alternating electromotive force (EMF).
The instantaneous value of the alternating EMF can be expressed as:
E(t)=E0sin(ωt)
where E0 is the peak EMF and ω is the angular frequency.
According to Ohm's law, the relationship between the voltage (E), current (I), and resistance (R) is given by:
E=I⋅R
From this, we can express the current (I) flowing through the resistor as:
I=ER
We substitute the expression for E(t) into the equation for current:
I(t)=E0sin(ωt)R
We can define the peak current I0 as:
I0=E0R
Therefore, the expression for instantaneous current becomes:
I(t)=I0sin(ωt)
From the derived equations, we see that both the instantaneous EMF and the current are sinusoidal functions of time. Since they are both represented by sine functions with the same argument (ωt), it follows that the EMF and the current are in phase. This means that when the EMF reaches its maximum value, the current also reaches its maximum value simultaneously.
This relationship can be represented graphically, where both the EMF (E) and the current (I) waveforms will have the same shape and peak at the same time.
In a pure resistor, the alternating current is directly proportional to the alternating EMF, and both quantities are in phase with each other. This means that there is no phase difference between the voltage across the resistor and the current flowing through it.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Exercies (Long Answer Questions)
12 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problems (Level - I)
16 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises (Long Answer Questions)
2 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
Similar Questions
What is the value of power factor for a pure resistor connected to an alternating current source?
View Solution(a) Discuss the heat flow through a composite slab.
(b) Derive an expression for the rate of increase of thickness of ice on a lake.
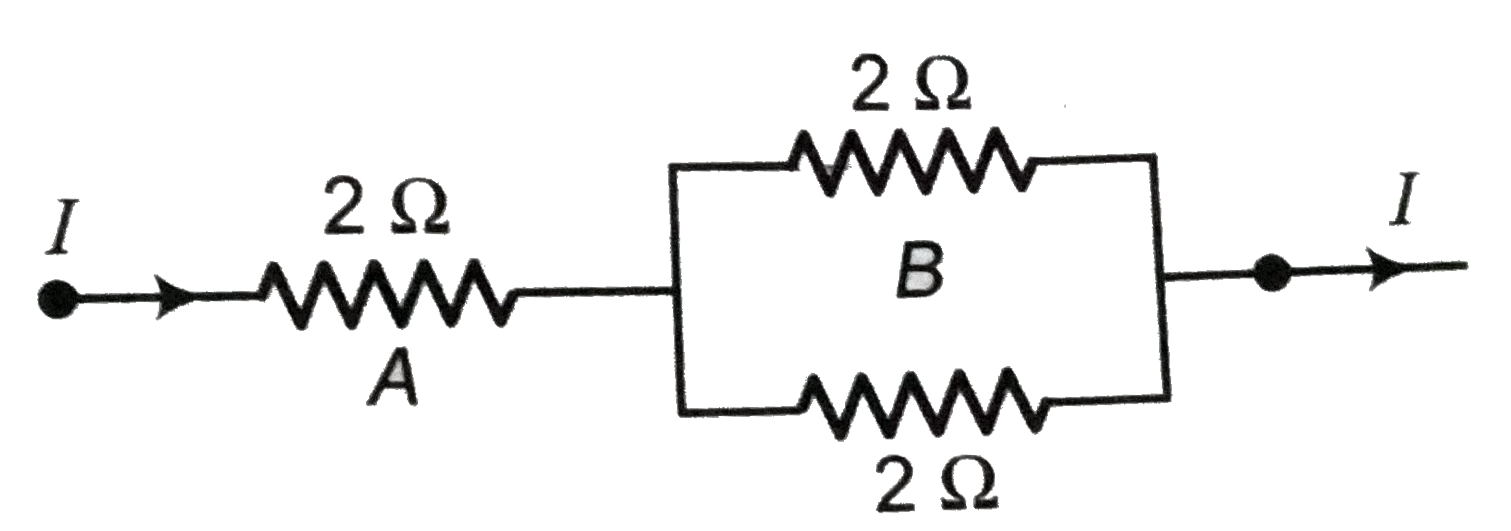
View SolutionThree 2Ω resistors, A, B and C are connected as shown in figure. Each of them dissipates energy and can with stand a maximum power of 18 W without melting. Find the maximum current that can flow through the three resistors ?
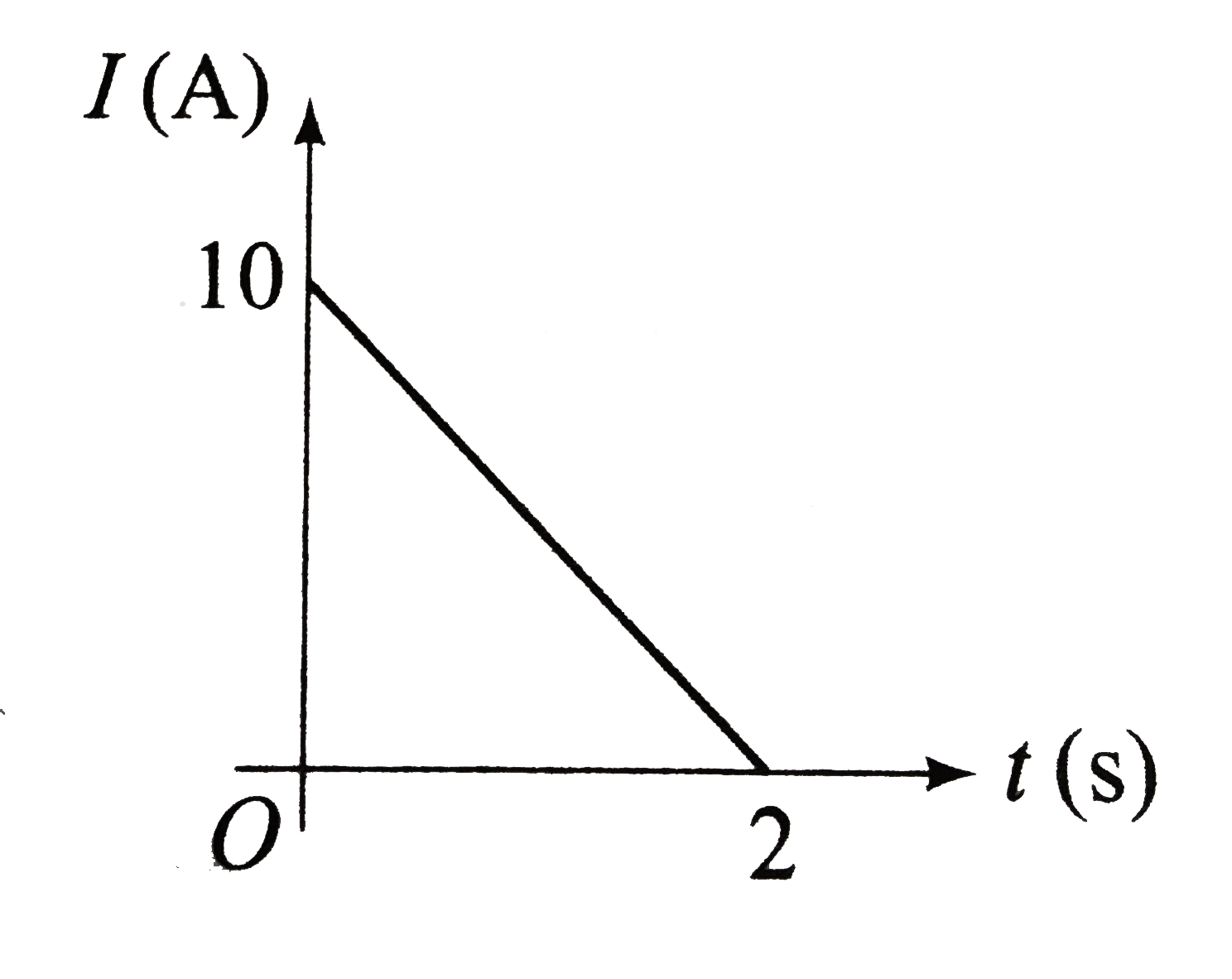
View SolutionA variable current flows through a 1Ω resistor for 2 s. Time dependence of the current is shown in the graph.
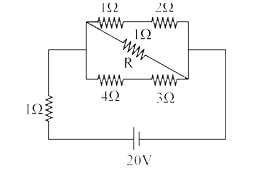
View SolutionFind the current through resistor R.
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionAn AC source is connected to a diode and a resistor in series. Is the current through the resistor AC or DC?
View SolutionCalculate the current flowing through each of the resistors A and B in the circuit shown in Fig.

View SolutionAn A.C. generator generating an emf E given by E = 311 sin(10t) is connected to a 44 Ω resistor. Calculate :
(i) rms value of A.C. flowing through the resistor.
(ii) frequency of the current
(iii)mean value of emf generated by the generator in time interval 0.06 to 0.08s.
View Solution
