Where is the power dissipation in an alternating current ? In resistance ? In inductance ? In capacitance ?
To determine where power dissipation occurs in an alternating current (AC) circuit, we can analyze the roles of resistance, inductance, and capacitance.
1. Understanding Power Dissipation:
- Power dissipation in electrical circuits refers to the conversion of electrical energy into heat or other forms of energy. In AC circuits, this is primarily associated with resistive components.
2. Power Formula:
- The formula for power dissipation in a resistive circuit is given by:
P=I2R
- Here, P is the power, I is the current, and R is the resistance. This equation indicates that power dissipation occurs due to the resistance in the circuit.
3. Reactive Power:
- In AC circuits, we also deal with inductance and capacitance, which do not dissipate power but rather store and release energy. The power associated with these components is known as reactive power.
- The formulas for reactive power are:
- For inductance: PL=I2XL
- For capacitance: PC=I2XC
- Here, XL and XC are the inductive and capacitive reactances, respectively. However, these do not contribute to power dissipation in the same way resistance does.
4. Conclusion:
- Since only resistive components convert electrical energy into heat (dissipate power), we conclude that power dissipation in an alternating current occurs solely in the resistance.
Final Answer:
Power dissipation in an alternating current occurs in the resistance only.
---
- Power dissipation in electrical circuits refers to the conversion of electrical energy into heat or other forms of energy. In AC circuits, this is primarily associated with resistive components.
- The formula for power dissipation in a resistive circuit is given by:
P=I2R
- Here, P is the power, I is the current, and R is the resistance. This equation indicates that power dissipation occurs due to the resistance in the circuit.
- In AC circuits, we also deal with inductance and capacitance, which do not dissipate power but rather store and release energy. The power associated with these components is known as reactive power.
- The formulas for reactive power are:
- For inductance: PL=I2XL
- For capacitance: PC=I2XC
- Here, XL and XC are the inductive and capacitive reactances, respectively. However, these do not contribute to power dissipation in the same way resistance does.
- Since only resistive components convert electrical energy into heat (dissipate power), we conclude that power dissipation in an alternating current occurs solely in the resistance.
Power dissipation in an alternating current occurs in the resistance only.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problems (Level - I)
16 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problem (Level - II)
9 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Exercies (Short Answer Questions)
4 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
Similar Questions
The power dissipated in the adjacent circuit is -
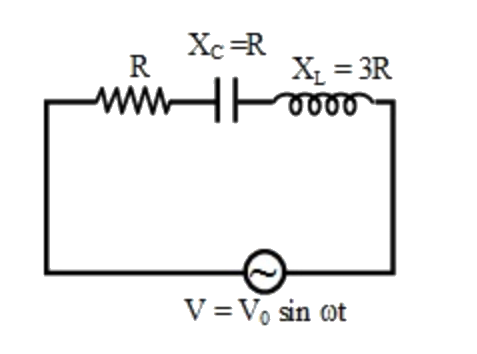
View SolutionThe average power dissipation in a pure capacitance in AC circuit is
View SolutionA choke coil of resistance 5Ω and inductance 0.6 H is in series with a capacitance of 10(μ)F. If a voltage of 200 V is applied and the frequency is adjusted to resonance, the current and voltage across the inductance and capacitance are (I0),(V0)and(V1) respectively. we have
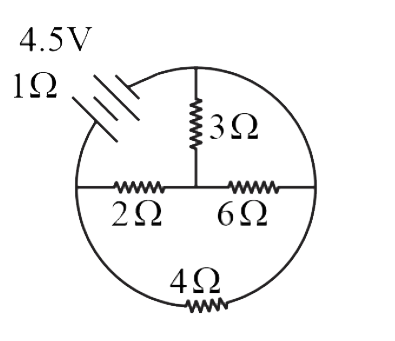
View SolutionThe power dissipated (in watt) in 3Ω resistance in the following circuit is
View SolutionThe average power dissipated in a pure inductor L carrying an alternating current of rms value I is .
View SolutionFigure shows the net power dissipated in R versus the current in a simple circuit shown.
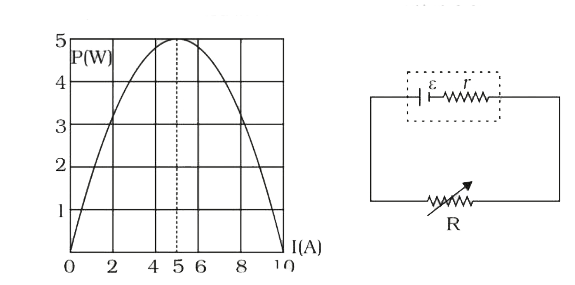
View SolutionThe average power is dissipated in a pure inductor is
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionPower dissipated in pure inductance will be-
View SolutionA choke coil is connected to an AC source. Some power is dissipated in coil. Now a capacitor is connected in series with the coil and source is same, then average power dissipated in the circuit does not changes. If ratio of inductive reactance of coil and capacitive reactance of capacitor is1x then find x
View Solution
