Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor
increase
decrease
does not change
is zero.
The correct Answer is:A, B
To solve the question regarding displacement current in a capacitor, we will follow these steps:
Step 1: Understand the Concept of Displacement Current
Displacement current is a concept introduced by James Clerk Maxwell to account for the changing electric field in regions where there is no conduction current, such as the gap between the plates of a capacitor. It is defined as:
Id=ϵ0dΦEdt
where Id is the displacement current, ϵ0 is the permittivity of free space, and ΦE is the electric flux.
Step 2: Relate Electric Flux to Charge
According to Gauss's law, the electric flux ΦE through a surface is related to the charge Q enclosed by that surface:
ΦE=Qϵ0
Substituting this into the displacement current equation gives:
Id=ϵ0ddt(Qϵ0)=dQdt
This shows that the displacement current is directly proportional to the rate of change of charge Q on the capacitor plates.
Step 3: Analyze the Options
1. If the charge increases: dQdt>0 → Displacement current exists.
2. If the charge decreases: dQdt<0 → Displacement current exists.
3. If the charge does not change: dQdt=0 → Displacement current is zero.
4. If the charge is zero: This is a special case, but if the charge is not changing, the displacement current is still zero.
Step 4: Conclusion
From the analysis, we conclude that the displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor is either increasing or decreasing. Therefore, the correct answers are:
- Option A: Increased charge → Displacement current exists.
- Option B: Decreased charge → Displacement current exists.
- Option C: Charge does not change → Displacement current is zero.
- Option D: Charge is zero → Displacement current is zero (if not changing).
Thus, the correct options are A and B.
Displacement current is a concept introduced by James Clerk Maxwell to account for the changing electric field in regions where there is no conduction current, such as the gap between the plates of a capacitor. It is defined as:
Id=ϵ0dΦEdt
where Id is the displacement current, ϵ0 is the permittivity of free space, and ΦE is the electric flux.
According to Gauss's law, the electric flux ΦE through a surface is related to the charge Q enclosed by that surface:
ΦE=Qϵ0
Substituting this into the displacement current equation gives:
Id=ϵ0ddt(Qϵ0)=dQdt
This shows that the displacement current is directly proportional to the rate of change of charge Q on the capacitor plates.
1. If the charge increases: dQdt>0 → Displacement current exists.
2. If the charge decreases: dQdt<0 → Displacement current exists.
3. If the charge does not change: dQdt=0 → Displacement current is zero.
4. If the charge is zero: This is a special case, but if the charge is not changing, the displacement current is still zero.
From the analysis, we conclude that the displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor is either increasing or decreasing. Therefore, the correct answers are:
- Option A: Increased charge → Displacement current exists.
- Option B: Decreased charge → Displacement current exists.
- Option C: Charge does not change → Displacement current is zero.
- Option D: Charge is zero → Displacement current is zero (if not changing).
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Question for short answers
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - objective 1
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
Similar Questions
A : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change.
R : Displacement current arises only when the electric field is constant.
View SolutionAn insulator plate is passed between the plates of a capacitor. Then current
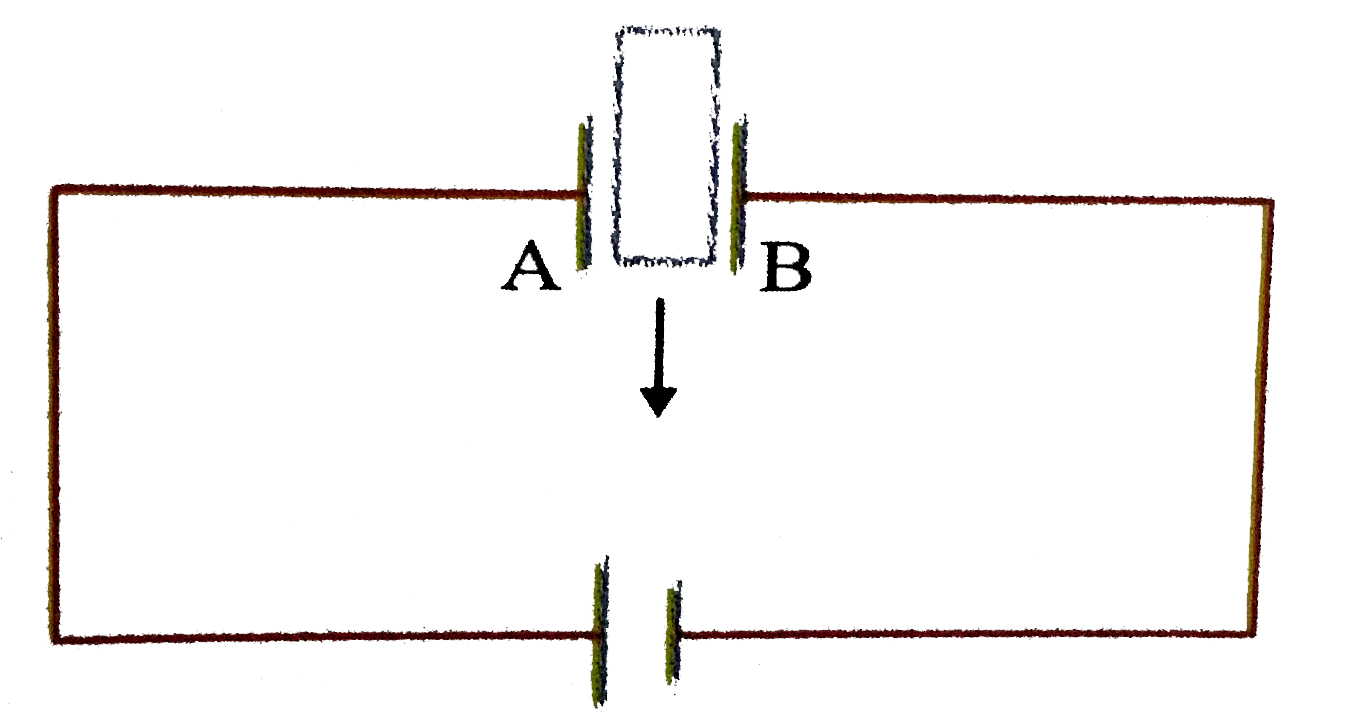 .
.
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
View SolutionTo establish an instantaneous displacement current of I ampere in the space between the plates of a parallel plate capacitor of 12 farad, the value of dVdt is
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionHow would you established an instantaneous displacement current of 4A in the space between the two parallel plates of 2μF capacitor.
View SolutionHow would you establish an instantaneous displacement current of 1 A in the space between the two parallel plates of a 2μF capacitor?
View SolutionForce of attraction between the plates of a parallel plate capacitor is
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View Solution