Displacement of a particle moving in a straight line is represented as follows:
Ratio of initial velocity to initial acceleration depends.
Only on a and b
Only on b and c
Only on c and d
Only on d and a
The correct Answer is:b
To find the ratio of initial velocity to initial acceleration for the given displacement function x=at3+bt2+ct+d, we will follow these steps:
Step 1: Find the expression for velocity
The velocity v is the first derivative of displacement x with respect to time t.
v=dxdt=ddt(at3+bt2+ct+d)
Step 2: Differentiate the displacement function
Using the power rule of differentiation, we differentiate each term:
- The derivative of at3 is 3at2
- The derivative of bt2 is 2bt
- The derivative of ct is c
- The derivative of the constant d is 0
Thus, the expression for velocity becomes:
v=3at2+2bt+c
Step 3: Calculate initial velocity
The initial velocity v0 is the value of velocity at t=0:
v0=v(0)=3a(0)2+2b(0)+c=c
Step 4: Find the expression for acceleration
Acceleration a is the derivative of velocity v with respect to time t:
a=dvdt=ddt(3at2+2bt+c)
Step 5: Differentiate the velocity function
Using the power rule again, we differentiate each term:
- The derivative of 3at2 is 6at
- The derivative of 2bt is 2b
- The derivative of c is 0
Thus, the expression for acceleration becomes:
a=6at+2b
Step 6: Calculate initial acceleration
The initial acceleration a0 is the value of acceleration at t=0:
a0=a(0)=6a(0)+2b=2b
Step 7: Find the ratio of initial velocity to initial acceleration
Now, we can find the ratio of initial velocity v0 to initial acceleration a0:
v0a0=c2b
Conclusion
The ratio of initial velocity to initial acceleration depends on the constants c and b in the displacement equation.
---
The velocity v is the first derivative of displacement x with respect to time t.
Using the power rule of differentiation, we differentiate each term:
- The derivative of bt2 is 2bt
- The derivative of ct is c
- The derivative of the constant d is 0
The initial velocity v0 is the value of velocity at t=0:
Acceleration a is the derivative of velocity v with respect to time t:
Using the power rule again, we differentiate each term:
- The derivative of 2bt is 2b
- The derivative of c is 0
The initial acceleration a0 is the value of acceleration at t=0:
Now, we can find the ratio of initial velocity v0 to initial acceleration a0:
The ratio of initial velocity to initial acceleration depends on the constants c and b in the displacement equation.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
74 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
13 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - REVISION EXERCISE (NUMERICAL PROBLEMS )
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
The displacement of a particle moving along a straight line is given by
s=3t^(3)+2t^(2)-10t. find initial velocity and acceleration of particle.
View SolutionThe displacement of a particle moving in a straight line is given by s=t3−6t2+3t+4 meters.The velocity when acceleration is zero is "
View Solution
Knowledge Check
Displacement of a particle moving in a straight line is written as follows:
x=t33−5t22+6t+7
what is the possible acceleration of particle when particle is in a state of rest?A1m/s2B−1m/s2C−5m/s2D+5m/s2Velocity displacement graph of a particle moving in a straight line is as shown in figure.
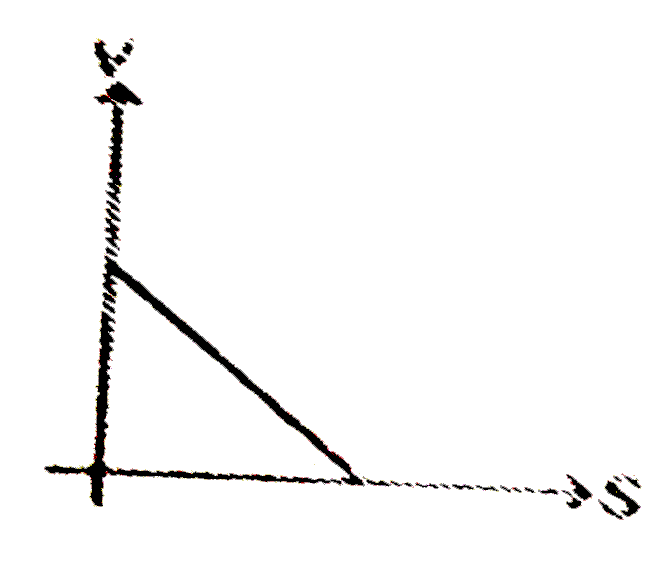 Amagnitude of acceleration of particle is decreasingBmagnitude of acceleration of particlre is increasingCacceleration versus displacement graph straight lineDacceleration versus displacement graph is parabola
Amagnitude of acceleration of particle is decreasingBmagnitude of acceleration of particlre is increasingCacceleration versus displacement graph straight lineDacceleration versus displacement graph is parabolaFor a particle moving along a straight line, the displacement x depends on time t as x=At3+Bt2+Ct+D. The ratio of its initial velocity to its initial acceleration depends on:
AA & CBB & CCCDC and D
The acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
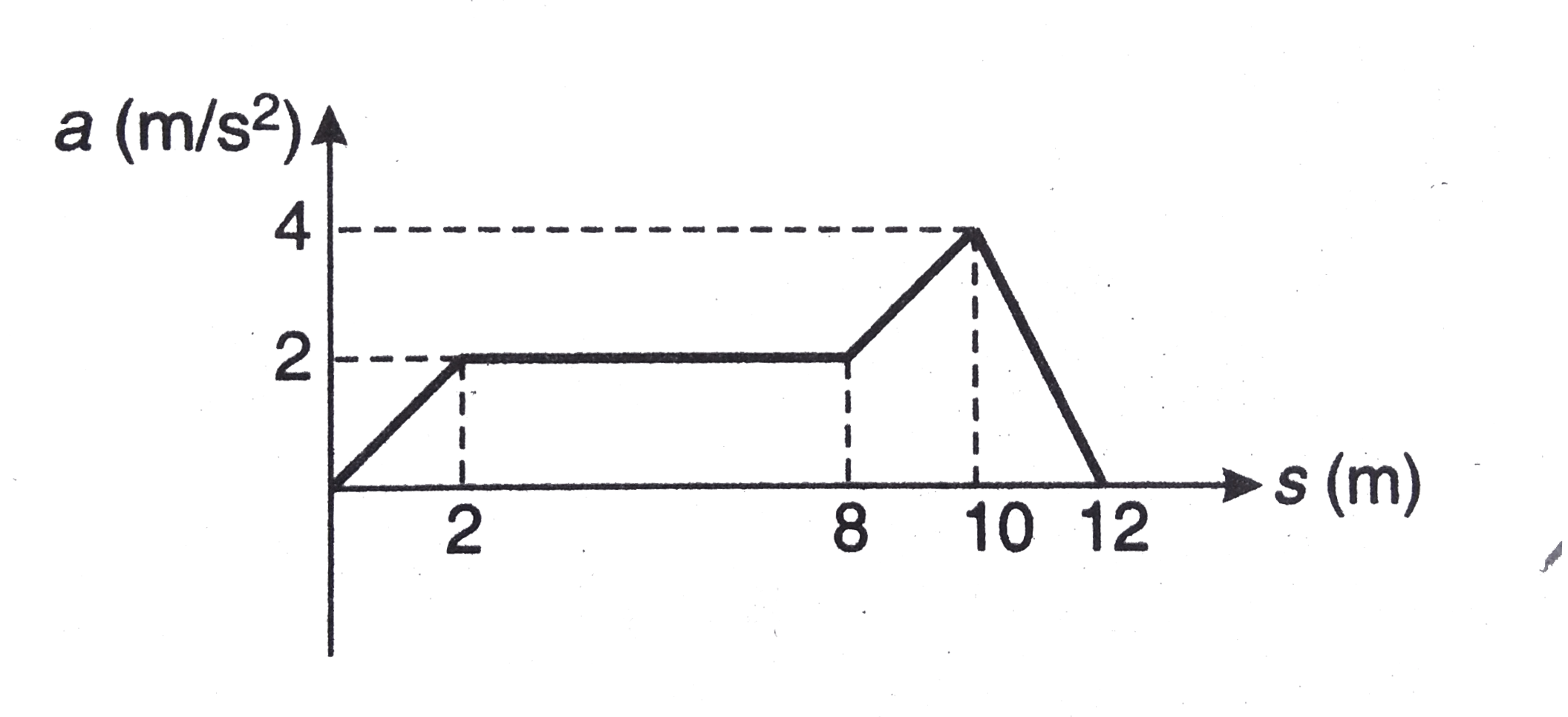
View SolutionA particle moves in a straight line as s=α(t−4)+β(t−4)2. Find the initial velocity and acceleration.
View SolutionA particle is moving in a straight line its speed depends on x as shown. The acceleration of particle is...
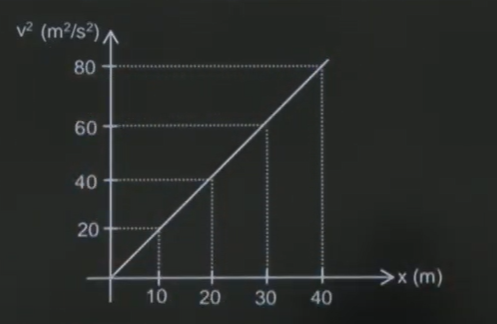
View SolutionA particle is moving on a straight line with constant retardation of 1m/s2. Its initial velocity is 10m/s.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View Solution
