Distance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
A
3h4
B
5h8
C
3h28R
D
h24R
Video Solution
Text Solution
The correct Answer is:A
All distances have to be taken from Z0 (the reference line) From similar triangle
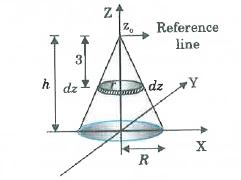
zr=hR
mass of small element of radius r
dm=M13πM2h×πr2dz
=3MπR2h×π(Rzh)2dz
dm=3Mh3×z2dz
Centre of mass lies on the Z-axis Take limit from 2 = 0 to Z =h
Zcm=1M∫z=hz=0z.dm=3h3∫h0z3.dz
=3h4
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
67 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
Distance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
Ab24RB3b4C5h8D3h28RThe radius of a circular cone is R and its height is H. The volume of cone is :
AπR2HB23πR2HCπR2H3DπRH2The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
View SolutionThe total surface area of a cone is 704 cm2 and the radius of its base is 7 cm . Find its slant height .
View SolutionFind the curved surface area of a cone, if its slant height is 60cm and the radius of its base is 21cm.
View SolutionFind the distance of centre of mass of a uniform cone of height 'h' and base radius R, from the vertex on the line of symmetry .
View SolutionThe centre of mass of a solid cone along the line form the center of the base to the vertex is at
View Solution
