Draw a diagram to illustrate the determination of the focal length of a convex lens using an auxiliary plane mirror.
To determine the focal length of a convex lens using an auxiliary plane mirror, we can follow these steps to draw the diagram and explain the setup:
1. Draw the Convex Lens: Start by drawing a convex lens in the center of your diagram. Label the lens as "Convex Lens".
2. Indicate the Optical Axis: Draw a horizontal line through the center of the lens to represent the optical axis. This line is crucial for understanding the path of light.
3. Place the Object: On one side of the lens, draw an arrow pointing upwards to represent the object. Label this object as "Object (O)". Place it at a distance greater than the focal length of the lens.
4. Draw the Auxiliary Plane Mirror: On the opposite side of the lens, draw a vertical line to represent the plane mirror. Label it as "Auxiliary Plane Mirror".
5. Draw the Image Formation: From the top of the object, draw two rays of light:
- One ray should travel parallel to the optical axis toward the lens and then refract through the focal point on the other side.
- The second ray should pass through the center of the lens and continue straight without bending.
6. Locate the Image: Extend the refracted rays backward to find the position of the image formed by the lens. Mark this point and label it as "Image (I)".
7. Indicate the Focal Length: Mark the focal points on both sides of the lens. Label the focal length as "F".
8. Label Distances: Indicate the distances:
- "u" for the object distance (distance from the object to the lens).
- "v" for the image distance (distance from the image to the lens).
9. Final Touches: Ensure all parts of the diagram are clearly labeled and that the rays are drawn accurately to show how they converge to form an image.
Diagram Summary:
- The diagram should clearly show the convex lens, the object, the auxiliary plane mirror, the rays of light, the image, and the focal points.
- One ray should travel parallel to the optical axis toward the lens and then refract through the focal point on the other side.
- The second ray should pass through the center of the lens and continue straight without bending.
- "u" for the object distance (distance from the object to the lens).
- "v" for the image distance (distance from the image to the lens).
- The diagram should clearly show the convex lens, the object, the auxiliary plane mirror, the rays of light, the image, and the focal points.
Topper's Solved these Questions
Similar Questions
Find the focal length of the lens used.
View SolutionThe given ray diagram illustrates the experimental set up for the determination of the focal length of a converging lens using a plane mirror.

write two characterisitics of the image formed
View SolutionThe given ray diagram illustrates the experimental set up for the determination of the focal length of a converging lens using a plane mirror.
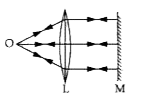
state the magnification of the image formed .
View SolutionThe given ray diagram illustrates the experimental set up for the determination of the focal length of a converging lens using a plane mirror.
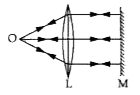
What is the name given to the distance between the object and optical centre of the lens in the given diagram?
View SolutionFocal length of a convex mirror is 10 cm
View SolutionIn an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
View SolutionDraw suitable diagrams to illustrate the action of (i) concave mirror, and (ii) convex mirror, on a beam of light incident parallel to the principal axis.
View SolutionDraw a diagram to show refraction of a plane wave front incident in a convex lens and hence draw the refracted wave front
View SolutionA concave lens of focal length 20 cm placed in contact with a plane mirror acts as a
View SolutionDefine the terms focus and focal length of a concave mirror. Draw diagram to illustrate your answer.
View Solution