Draw the electric field vs distance (from the centre ) graph for (i) a long charged rod having linear charge density λ>0 (ii) spherical shell of radius R and charge Q>0 .
To solve the problem of drawing the electric field vs. distance graph for (i) a long charged rod with linear charge density λ>0 and (ii) a spherical shell of radius R with charge Q>0, we will analyze each case step by step.
Step 1: Electric Field due to a Long Charged Rod
1. Understanding the Electric Field Formula:
The electric field E at a distance r from a long charged rod with linear charge density λ is given by the formula:
E=2kλr
where k is Coulomb's constant.
2. Behavior of Electric Field:
- As r approaches 0, E approaches infinity.
- As r increases, E decreases and approaches 0 as r approaches infinity.
3. Graphing the Electric Field:
- On the x-axis, plot the distance r from the center of the rod.
- On the y-axis, plot the electric field E.
- The graph will start from infinity at r=0 and will asymptotically approach 0 as r increases.
Step 2: Electric Field due to a Spherical Shell
1. Understanding the Electric Field Inside and Outside the Shell:
- For a conducting spherical shell with charge Q>0:
- Inside the shell (i.e., r<R): The electric field E=0.
- On the surface of the shell (i.e., r=R): The electric field is given by:
E=kQR2
- Outside the shell (i.e., r>R): The electric field is given by:
E=kQr2
2. Behavior of Electric Field:
- For r<R, E=0.
- At r=R, E reaches a maximum value of kQR2.
- For r>R, E decreases as 1r2.
3. Graphing the Electric Field:
- On the x-axis, plot the distance r from the center of the shell.
- On the y-axis, plot the electric field E.
- The graph will be 0 for r<R, jump to kQR2 at r=R, and then decrease as 1r2 for r>R.
Final Graphs
1. For the Long Charged Rod:
- The graph starts from infinity at r=0 and decreases towards 0 as r increases.
2. For the Spherical Shell:
- The graph is 0 for r<R, jumps to kQR2 at r=R, and then decreases towards 0 as r approaches infinity.
The electric field E at a distance r from a long charged rod with linear charge density λ is given by the formula:
E=2kλr
where k is Coulomb's constant.
- As r approaches 0, E approaches infinity.
- As r increases, E decreases and approaches 0 as r approaches infinity.
- On the x-axis, plot the distance r from the center of the rod.
- On the y-axis, plot the electric field E.
- The graph will start from infinity at r=0 and will asymptotically approach 0 as r increases.
- For a conducting spherical shell with charge Q>0:
- Inside the shell (i.e., r<R): The electric field E=0.
- On the surface of the shell (i.e., r=R): The electric field is given by:
E=kQR2
- Outside the shell (i.e., r>R): The electric field is given by:
E=kQr2
- For r<R, E=0.
- At r=R, E reaches a maximum value of kQR2.
- For r>R, E decreases as 1r2.
- On the x-axis, plot the distance r from the center of the shell.
- On the y-axis, plot the electric field E.
- The graph will be 0 for r<R, jump to kQR2 at r=R, and then decrease as 1r2 for r>R.
- The graph starts from infinity at r=0 and decreases towards 0 as r increases.
- The graph is 0 for r<R, jumps to kQR2 at r=R, and then decreases towards 0 as r approaches infinity.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)
59 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
Knowledge Check
Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2A charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
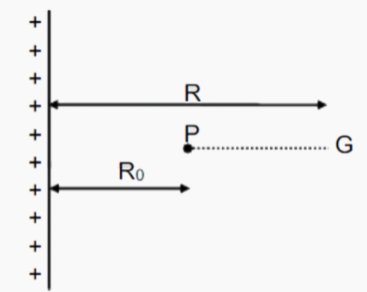 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
AEB3E2CE2DZero
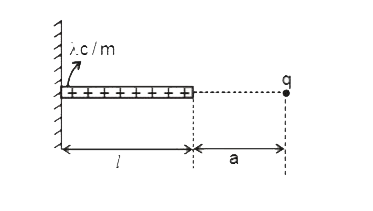
Find the total force on charge q due to a charge rod having linear charge density λCm placed as shown in figure.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionElectric potential at the centre of a spherical shell of radius r and having charge g is given as ___________ .
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View Solution
