An oil drop of mass m carrying charge - Q is to be held stationary in the gravitational field of the earth. What is the magnitude and direction of the electrostatic field required for this purpose ?
To solve the problem of holding an oil drop of mass m carrying charge −Q stationary in the gravitational field of the Earth, we need to analyze the forces acting on the drop.
1. Identify the Forces Acting on the Oil Drop:
- The oil drop experiences a gravitational force acting downward, which is given by:
Fg=mg
where g is the acceleration due to gravity.
2. Condition for Stationarity:
- For the oil drop to remain stationary, the net force acting on it must be zero. This means that the upward electrostatic force must balance the downward gravitational force:
Fe=Fg
Hence, we have:
Fe=mg
3. Electrostatic Force on the Oil Drop:
- The electrostatic force Fe acting on a charge −Q in an electric field E is given by:
Fe=−Q⋅E
Since the charge is negative, the direction of the electrostatic force is opposite to the direction of the electric field.
4. Setting Up the Equation:
- To keep the drop stationary, we equate the magnitudes of the gravitational force and the electrostatic force:
−Q⋅E=mg
Since we are interested in the magnitude of the electric field, we can ignore the negative sign for now:
Q⋅E=mg
5. Solving for the Electric Field E:
- Rearranging the equation to find the magnitude of the electric field E:
E=mgQ
6. Determining the Direction of the Electric Field:
- Since the oil drop has a charge of −Q and the electrostatic force must act upward to balance the weight (which acts downward), the electric field must be directed downward. This is because the force on a negative charge in an electric field is in the opposite direction to the field.
Final Answer:
- Magnitude of the Electric Field:
E=mgQ
- Direction of the Electric Field: Downward.
- The oil drop experiences a gravitational force acting downward, which is given by:
Fg=mg
where g is the acceleration due to gravity.
- For the oil drop to remain stationary, the net force acting on it must be zero. This means that the upward electrostatic force must balance the downward gravitational force:
Fe=Fg
Hence, we have:
Fe=mg
- The electrostatic force Fe acting on a charge −Q in an electric field E is given by:
Fe=−Q⋅E
Since the charge is negative, the direction of the electrostatic force is opposite to the direction of the electric field.
- To keep the drop stationary, we equate the magnitudes of the gravitational force and the electrostatic force:
−Q⋅E=mg
Since we are interested in the magnitude of the electric field, we can ignore the negative sign for now:
Q⋅E=mg
- Rearranging the equation to find the magnitude of the electric field E:
E=mgQ
- Since the oil drop has a charge of −Q and the electrostatic force must act upward to balance the weight (which acts downward), the electric field must be directed downward. This is because the force on a negative charge in an electric field is in the opposite direction to the field.
- Magnitude of the Electric Field:
E=mgQ
- Direction of the Electric Field: Downward.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS
49 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
What is the magnitude and direction of force on an electron moving along the direction of the magnetic field.
View SolutionOn an imaginary planet the acceleration due to gravity is same as that on Earth but there is also a downward electric field that is uniform close to the planet's surface. A ball of mass m carrying a charge q is thrown upward at a speed v and hits the ground after an interval t, What is the magnitude of potential difference between the starting point and top point of the trajectory?
View Solution
Knowledge Check

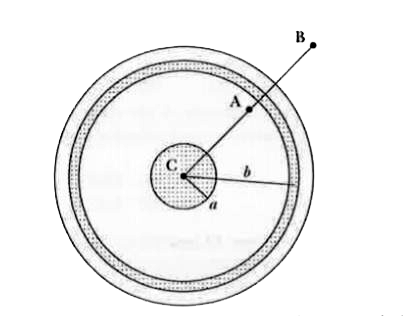 What is the magnitude and direction of the magnetic field at point B ?A3.3×10−5 T, clockwiseB6.8×10−5 T, counterclockwiseC3.3×10−5 T, counterclockwiseD2.7×10−4 T, clockwise
What is the magnitude and direction of the magnetic field at point B ?A3.3×10−5 T, clockwiseB6.8×10−5 T, counterclockwiseC3.3×10−5 T, counterclockwiseD2.7×10−4 T, clockwise

What is the magnitude and direction of the magnetic field at point A ?A3.3×10−5 T, clockwiseB6.8×10−5 T, counterclockwiseC3.3×10−5 T, counterclockwiseD2.7×10−4 T, clockwiseIn Q.30, the magnitude and direction of magnetic field will be
A2.5μT in X-directionB2.5μT in Y-directionC2.5μT in Z-directionDNone of these
An oil drop of radius r carrying a charge q remain stationary in the presence of electric field of intensity E. If the density of oil ρ , then
View SolutionA positive charge particle with charge q is moving with speed v in a region of uniform magnetic field B at the instant shown in figure. An external electric field so to be applied so that the charged particle follows a straight line path. The magnitude and direction of electric field required are respectively.

View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionAt what height the gravitational field reduces by 75 % the gravitational field at the surface of earth ?
View SolutionA Water of mass 3.2×10−18kg and carrying a charge of 1.6×10−19C is suspended stationary betwaeen two plates of an electric field. Given g=10m/s2, the intensity of the electric field required is
View Solution