During a process carried on an ideal gas it was found that η(<1) times the heat supplied to the gas is equal to increase in internal energy of the gas. Write the process equation in terms of pressure (P) and volume (V) of the gas. It is given that ratio of specific heats for the gas is CPCV=γ.
The correct Answer is:PV[1−η(γ−1)(1−η)]
Step by step video, text & image solution for During a process carried on an ideal gas it was found that eta (lt 1) times the heat supplied to the gas is equal to increase in internal energy of the gas. Write the process equation in terms of pressure (P) and volume (V) of the gas. It is given that ratio of specific heats for the gas is (C_(P))/(C_(V)) = gamma. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
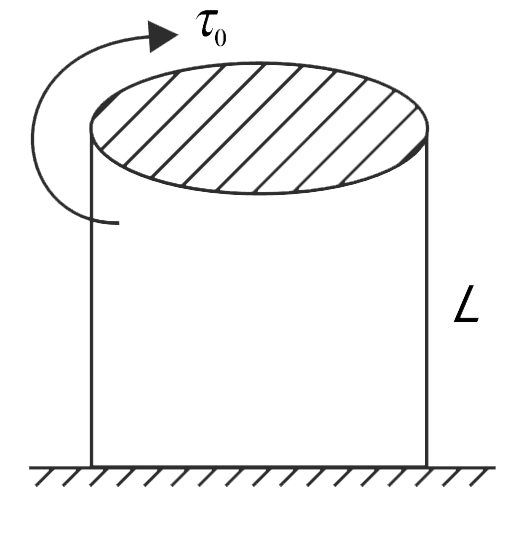
View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
View SolutionWe know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
View SolutionIf γ be the ratio of specific heats (Cp&Cv) for a perfect gas. Find the number of degrees of freedom of a molecules of the gas?
View SolutionDuring an adiabatic process of an ideal gas, if P is proportional to (1)/(V^(1.5) , then the ratio of specific heat capacities at constant pressure to that at constant volume for the gas is
View SolutionFor an ideal gas the ratio of specific heats is (C_(p))/(C_(v)) = gamma . The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
View SolutionAn ideal gas with heat capacity at constant volume C_(V) undergoes a quasistatic process described by P V^(alpha) in a P-V diagram, where alpha is a constant. The heat capacity of the gas during this process is given by-
View SolutionAn ideal gas (C_(P)//C_(V)=gamma) is expanded so that the amount of heat transferred to the gas the is equal to the decrease in its internal energy . What is the molar heat capacity of gas in this process ?
View SolutionAn ideal gas (C_(P)//C_(V)=gamma) is expanded so that the amount of heat transferred to the gas the is equal to the decrease in its internal energy . What is the relationship between temperature and volume of gas in this process ?
View SolutionIn a thermodynamic process on an ideal diatomic gas, work done by the gas is η times. The heat supplied (η<1). The molar heat capacity of the gas for the process is
View SolutionThe molar specific heat of an ideal gas at constant pressure and constant volume is C_(p) and C_(v) respectively. If R is the universal gas constant and the ratio of C_(p) to C_(v) is gamma , then C_(v) .
View Solutionएक आदर्श गैस के लिए रुद्धोष्म प्रक्रम में ताप T और दाब P में संबंध दर्शाने वाला समीकरण है ( जहाँ γ= गैस की दो विशिष्ट ऊष्माओ Cp और Cv का अनुपात=CpCv )
View Solutionकिसी आदर्श गैस की विशिष्ट ऊष्मा धारिताएँ नियत दाब तथा आयतन पर क्रमशः CpतथाCv है। यदि γ=CpCv तथा सार्वत्रिक गैस नियतांक R हो तो Cv बराबर है -
View SolutionThe molar specific heats of an ideal gas at constant pressure and volume are denotes by CP and Cυ respectively. If γ=CPCυ and R is the universal gas constant, then Cυ is equal to
View Solution
