For an ideal gas the ratio of specific heats is . The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding.
The correct Answer is:
Step by step video, text & image solution for For an ideal gas the ratio of specific heats is (C_(p))/(C_(v)) = gamma. The gas undergoes a polytropic process PV^(n) = a constant. Find the values of n for which the temperature of the gas increases when it rejects heat to the surrounding. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBook:ARIHANTChapter:FIRST LAW OF THERMODYNAMICSExercise:Level 2
Explore 34 Videos
- FIRST LAW OF THERMODYNAMICSBook:ARIHANTChapter:FIRST LAW OF THERMODYNAMICSExercise:Level 3
Explore 6 Videos
- ELASTICITYBook:ARIHANTChapter:ELASTICITYExercise:Level 3
Explore 1 Video
- FLUIDSBook:ARIHANTChapter:FLUIDSExercise:All Questions
Explore 70 Videos
Similar Questions
Knowledge Check
The ratio of the specific heats of a gas is CpCv=1.66 then the gas may be
ACO2BHeCH2DNO2P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
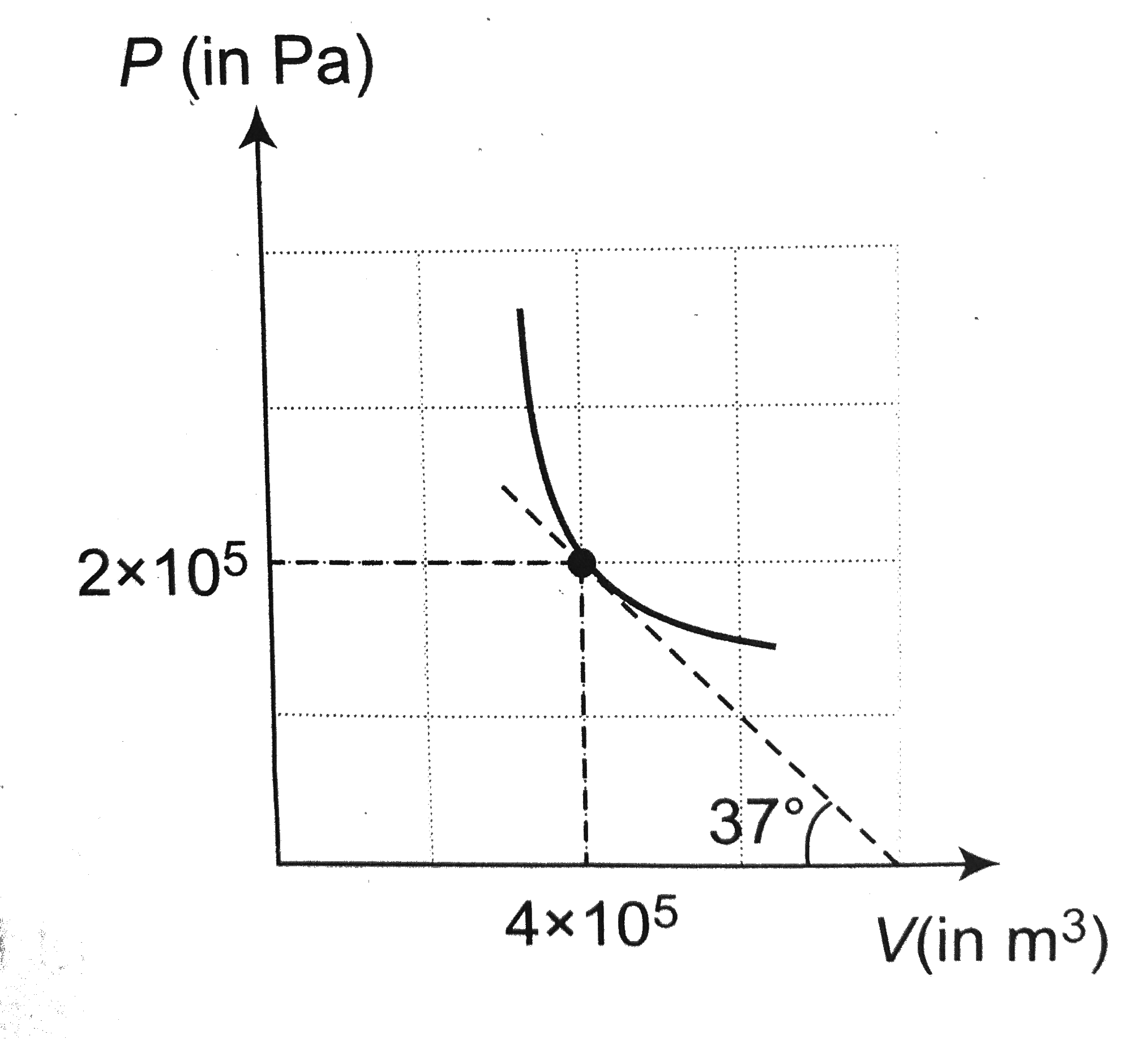 A34B−32C53D32
A34B−32C53D32One mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
ARΔTB3RΔTC5RΔTD6RΔT
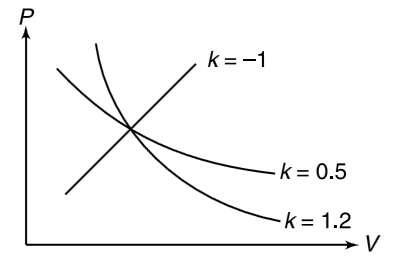
Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
View SolutionOne mole of an ideal gas with the adiabatic exponent γ goes through a polytropic process as a result of which the absolute temperature of the gas increases τ−fold. The polytropic constant equal n. Find the entropy increment of the gas in this process.
View SolutionFor polytropic process PVn = constant, molar heat capacity (Cm) of an ideal gas is given by:
View SolutionFigure demonstrates a polytropic process (i.e.PVn = constant ) for an ideal gas. The work done by the gas be in the process AB is
_S01_086_Q01.png)
View SolutionThe specific heat of a gas in a polytropic process is given by-
View Solution
