Each of four pairs of light waves arrives at a certain point on a screen. The waves have the same wavelength. At the arrival point, their amplitudes and phase differences are (a) 2E0,6E0, and π rad, (b) 3E0,5E0, and π rad, (c) 9E0,7E0 and 3π rad, (d) 2E0,2E0 and 0 rad. Rank the four pairs according to the intensity of the light at the arrival point, greatest first. (Hint: Draw phasors.)
To solve the problem of ranking the intensity of light at a certain point on the screen for the four pairs of light waves, we will use the principle of superposition and the formula for the resultant amplitude when two waves interfere. The intensity of light is proportional to the square of the resultant amplitude.
1. Understanding the Problem:
We have four pairs of light waves characterized by their amplitudes and phase differences. We need to find the resultant amplitude for each pair and then rank them according to their intensity.
2. Formula for Resultant Amplitude:
The resultant amplitude A when two waves with amplitudes A1 and A2 and a phase difference ϕ interfere is given by:
A=√A21+A22+2A1A2cos(ϕ)
3. Calculating Resultant Amplitude for Each Pair:
- Pair (a): Amplitudes 2E0,6E0 and phase difference π rad.
Aa=√(2E0)2+(6E0)2+2(2E0)(6E0)(cos(π))
Aa=√4E20+36E20−24E20=√16E20=4E0
- Pair (b): Amplitudes 3E0,5E0 and phase difference π rad.
Ab=√(3E0)2+(5E0)2+2(3E0)(5E0)(cos(π))
Ab=√9E20+25E20−30E20=√4E20=2E0
- Pair (c): Amplitudes 9E0,7E0 and phase difference 3π rad.
Ac=√(9E0)2+(7E0)2+2(9E0)(7E0)(cos(3π))
Ac=√81E20+49E20−126E20=√4E20=2E0
- Pair (d): Amplitudes 2E0,2E0 and phase difference 0 rad.
Ad=√(2E0)2+(2E0)2+2(2E0)(2E0)(cos(0))
Ad=√4E20+4E20+8E20=√16E20=4E0
4. Resultant Amplitudes Summary:
- Aa=4E0
- Ab=2E0
- Ac=2E0
- Ad=4E0
5. Ranking the Intensity:
The intensity is proportional to the square of the amplitude:
- Intensity for Pair (a): Ia∝(4E0)2=16E20
- Intensity for Pair (b): Ib∝(2E0)2=4E20
- Intensity for Pair (c): Ic∝(2E0)2=4E20
- Intensity for Pair (d): Id∝(4E0)2=16E20
Thus, the ranking according to intensity is:
- Aa=Ad>Ab=Ac
Final Ranking:
1. Pair (a) and Pair (d) (both have the same intensity)
2. Pair (b) and Pair (c) (both have the same intensity)
We have four pairs of light waves characterized by their amplitudes and phase differences. We need to find the resultant amplitude for each pair and then rank them according to their intensity.
The resultant amplitude A when two waves with amplitudes A1 and A2 and a phase difference ϕ interfere is given by:
A=√A21+A22+2A1A2cos(ϕ)
Aa=√(2E0)2+(6E0)2+2(2E0)(6E0)(cos(π))
Aa=√4E20+36E20−24E20=√16E20=4E0
Ab=√(3E0)2+(5E0)2+2(3E0)(5E0)(cos(π))
Ab=√9E20+25E20−30E20=√4E20=2E0
Ac=√(9E0)2+(7E0)2+2(9E0)(7E0)(cos(3π))
Ac=√81E20+49E20−126E20=√4E20=2E0
Ad=√(2E0)2+(2E0)2+2(2E0)(2E0)(cos(0))
Ad=√4E20+4E20+8E20=√16E20=4E0
- Aa=4E0
- Ab=2E0
- Ac=2E0
- Ad=4E0
The intensity is proportional to the square of the amplitude:
- Intensity for Pair (a): Ia∝(4E0)2=16E20
- Intensity for Pair (b): Ib∝(2E0)2=4E20
- Intensity for Pair (c): Ic∝(2E0)2=4E20
- Intensity for Pair (d): Id∝(4E0)2=16E20
- Aa=Ad>Ab=Ac
1. Pair (a) and Pair (d) (both have the same intensity)
2. Pair (b) and Pair (c) (both have the same intensity)
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS61videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)66videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Similar Questions
Light waves from two coherent source arrive at two points on a screen with path difference 0andλ/2. Find the ratio of intensities at the points.
View SolutionTwo coherent sources emit light waves which superimpose at a point where these can be expressed as
E1=E0sin(ωt+π/4)
E2=2E0sin(ωt−π/4)
Here, E1andE2 are the electric field strenghts of the two waves at the given point.
If I is the intensity of wave expressed by field strenght E1, find the resultant intensityView Solution
Knowledge Check
- Question 1 - Select One
Two light waves arrives at a certain point on a screen. The waves have the same wavelength. At the arrival point, their amplitudes and phase differences are :
(I) 2a0,6a0 and π rad (II)3a0,5a0 and π and
(III) 9a_(0), 7a_(0), " and "3pi " rad"(IV)2a0,2a0 and 0.
The pair/s which has greatest intensity is/are :AIBIICII,IIIDI, IV - Question 2 - Select One
The phase difference between the two light waves arriving point is 2nπradians. The condition for maximum intensity of light at that point is
AImax=a1+a2BImax=(a1+a2)2CImax=a1a2DImax=a1+a2a1−a2 - Question 3 - Select One
Two alternating voltage generators produce emfs of the same amplitude(E0) but with a phase difference of (π)/3. The resultant emf is
A(A) E0sin[ωt+(π)/3)]B(B) E0sin[ωt+(π)/6)]C(C) √3E0sin[ωt+(π)/6)]D(D) √3E0sin[ωt+(π)/2)]
Three light waves combine at a certain point where thcir electric field components are
E1=E0sinωt,
E2=E0sin(ωt+60∘),
E3=E0sin(ωt−30∘).
Find their resultant component E(t) at that point.View SolutionFour harmonic waves of equal freuencied and equal intensity I0 have phase angles 0,π3,2π3 and π. When they are superposed, the intensity of the resulting wave is nI0. The value of n is
View SolutionDetermine electric field at point P or O in the following cases , take 14π∈0.Qd2=E0.
(a)
(b)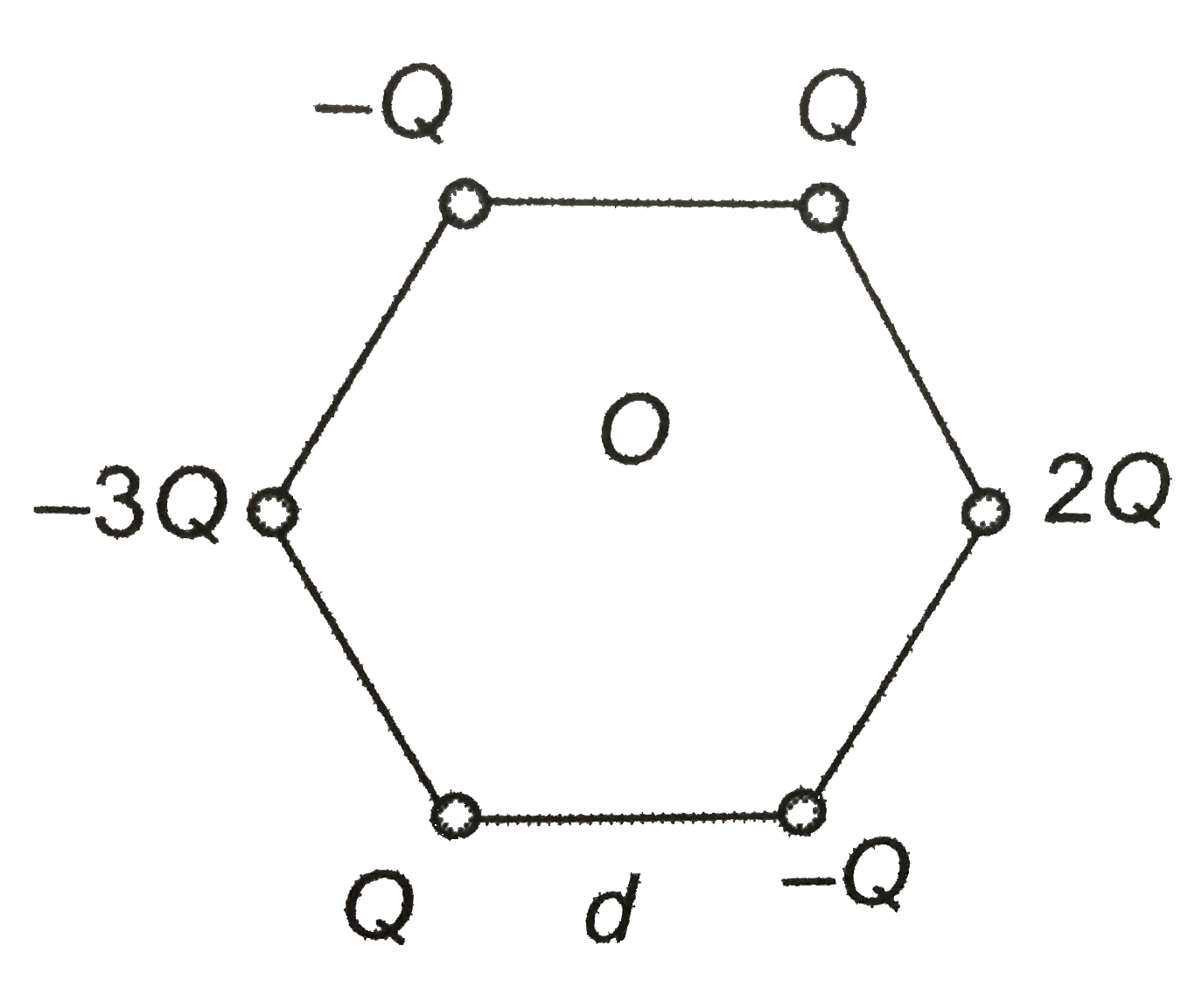 View Solution
View SolutionTwo waves at a point are represented by E1=E0sinωtandE2=E0sin(ω+ϕ). There will eb destructive interference at this point is
View SolutionThe following travelling electromagnetic wave Ex=0,Ey=E0sin(kx+ωt),Ez=–2E0sin(kx+ωt) is-
View Solution

