Effect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2
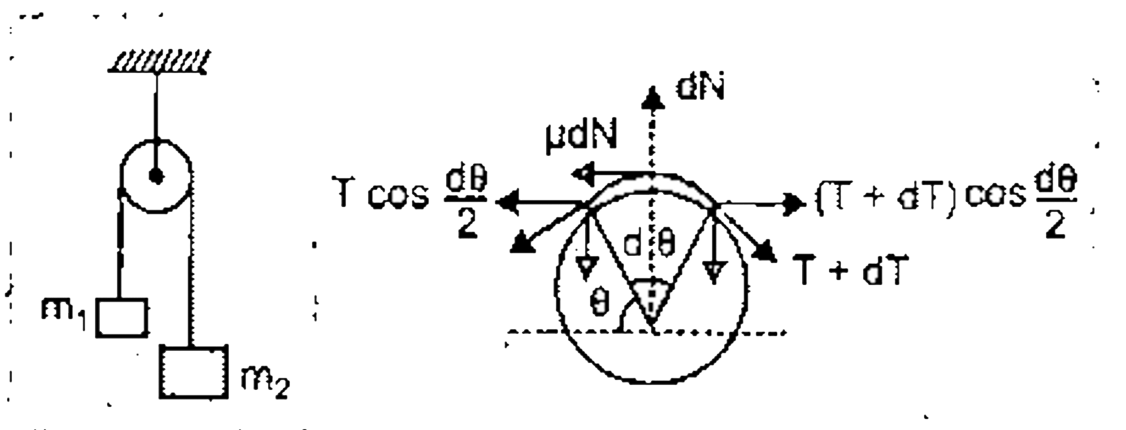
(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi
The tension on side of lighter mass will be:
A
m1g
B
m2g
C
2m2g3
D
4m1g3
Text Solution
The correct Answer is:d
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-273videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
Similar Questions
Knowledge Check
- Question 1 - Select One
Effect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2

(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi
The tension on side ofheavier\nass will be:Am1gBm2gC2m2g3D2m1g3 - Question 2 - Select One
Effect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2
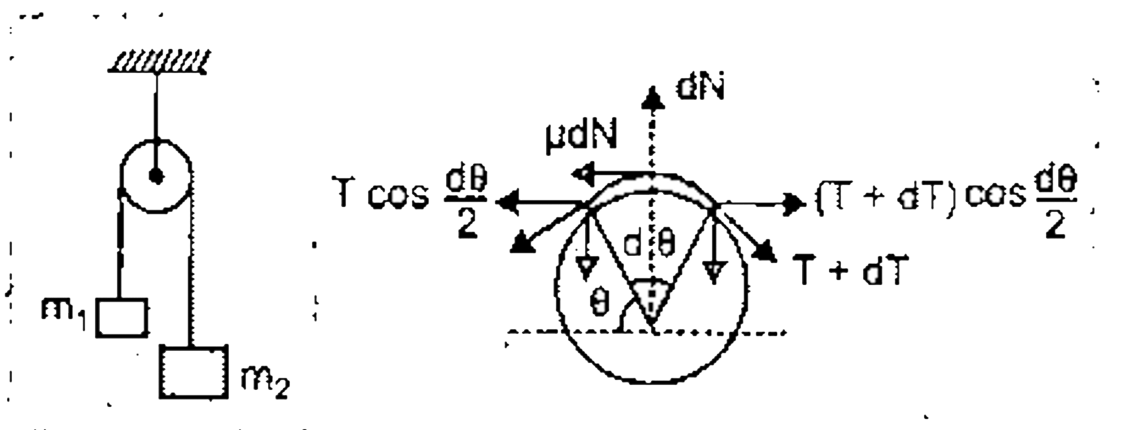
(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi<br>Ifm_(2)=2em then acceleration of each mass is :AgBg/3Ceg/3Dzero - Question 3 - Select One
Effect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient μ. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
dN=(T+dT)sindθ2+Tsindθ2

(T+dT)cosdθ2−Tcosdθ2−μdN=dra=0 (massless strings)
dTcosdθ2=μdN
dTcosdθ2=μ[(T+dt)sindθ2+Tsindθ2]
dt.cosdθ2=μ[Tsindθ2+dT.sindθ2+Tsindθ2]
dT=μ[T.dθ2+0+Tdθ2]=μTcosθ
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)<br>Supposecofficientofictionbetweenthestr∈gandp≤––––yismu =1/pi
What should be the ratio of heavier mass to lighter mass for no motion ?AeB1eCeLDeR
Find the acceleration and tension in the string in the following cases . The pulley and string are massless.
(a)
(b) View Solution
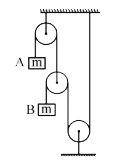
View SolutionIn the arrangement shown, the pulleys and strings are massless. The acceleration of block B is :
 View Solution
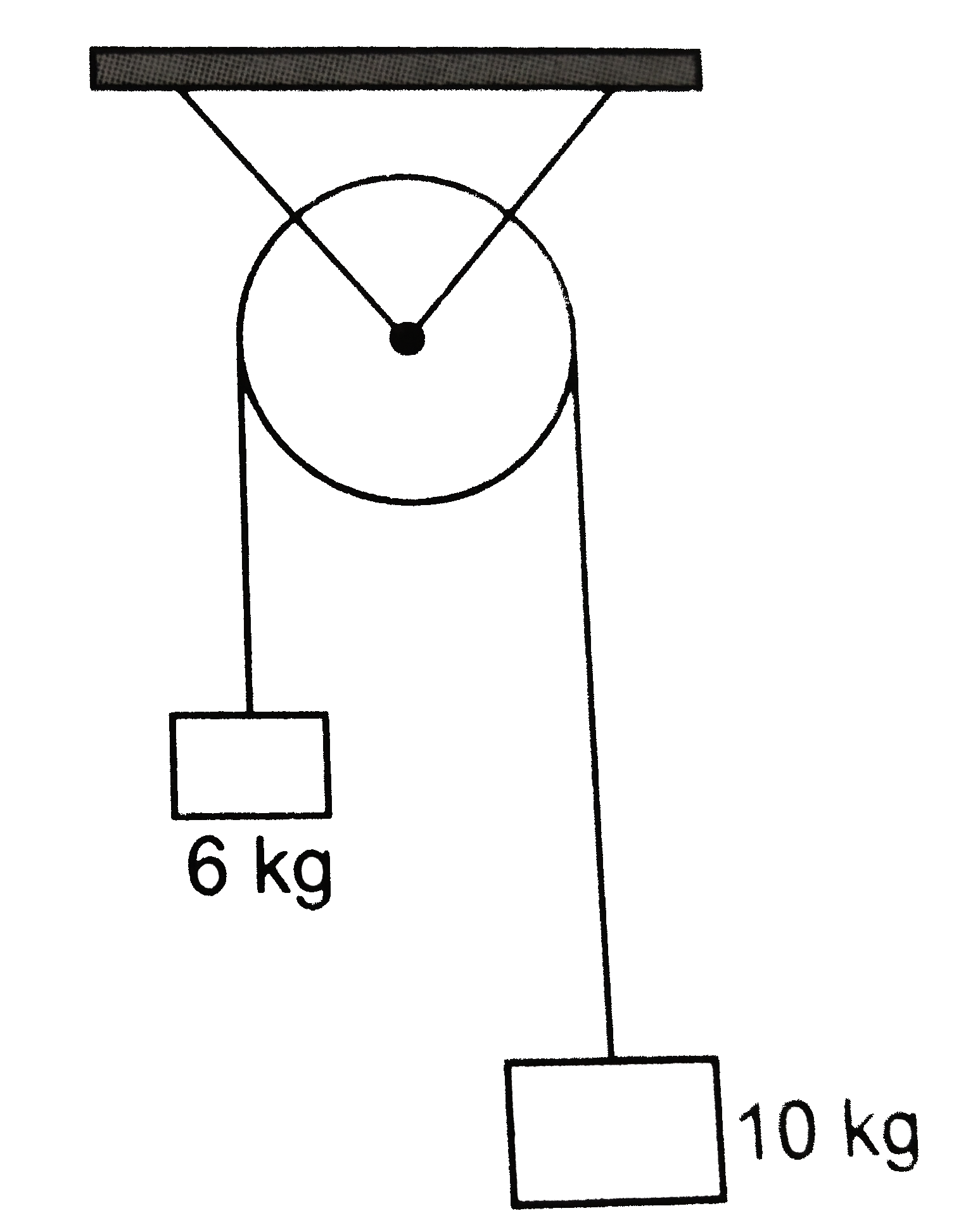
View SolutionThe tension in the string in the pulley system shown in
 .View Solution
.View SolutionPulleys and strings are massless. The horizontal surface is smooth. What is the acceleration of the block
 View Solution
View SolutionPulleys and strings are massless.The horizontal surface is smooth.What is the acceleration of the block
 View Solution
View Solution


