Electric current through a conductor varies with time as I(t)=50sin(100πt). Here I is in amperes and t in seconds. Total charge that passes any point from t=0 to t=1200s is
1.2 C
0.36 C
0.159 C
0.02 C
The correct Answer is:C
To find the total charge that passes through a point from t=0 to t=1200 seconds when the current is given by I(t)=50sin(100πt), we can follow these steps:
Step 1: Understand the relationship between current and charge
The current I(t) is defined as the rate of flow of charge Q with respect to time t. Mathematically, this is expressed as:
I(t)=dQdt
Thus, the total charge Q that passes through a point during a time interval can be found by integrating the current over that interval:
Q=∫t2t1I(t)dt
Step 2: Set up the integral
In our case, we need to integrate the current from t=0 to t=1200:
Q=∫1200050sin(100πt)dt
Step 3: Compute the integral
To solve the integral, we can factor out the constant:
Q=50∫12000sin(100πt)dt
Now, we will compute the integral of sin(100πt):
∫sin(100πt)dt=−1100πcos(100πt)+C
Now, we can evaluate the definite integral:
Q=50(−1100πcos(100πt))12000
Step 4: Evaluate the limits
Substituting the limits into the integral:
Q=50(−1100π(cos(100π⋅1200)−cos(100π⋅0)))
Calculating the cosine values:
cos(100π⋅1200)=cos(π2)=0
cos(0)=1
Thus, we have:
Q=50(−1100π(0−1))=50(1100π)
Q=50100π=12π
Step 5: Calculate the numerical value
To find the numerical value of Q:
Q≈12⋅3.14≈0.159Coulombs
Final Answer
The total charge that passes any point from t=0 to t=1200 seconds is approximately:
Q≈0.159C
---
The current I(t) is defined as the rate of flow of charge Q with respect to time t. Mathematically, this is expressed as:
I(t)=dQdt
Thus, the total charge Q that passes through a point during a time interval can be found by integrating the current over that interval:
Q=∫t2t1I(t)dt
In our case, we need to integrate the current from t=0 to t=1200:
Q=∫1200050sin(100πt)dt
To solve the integral, we can factor out the constant:
Q=50∫12000sin(100πt)dt
Now, we will compute the integral of sin(100πt):
∫sin(100πt)dt=−1100πcos(100πt)+C
Now, we can evaluate the definite integral:
Q=50(−1100πcos(100πt))12000
Substituting the limits into the integral:
Q=50(−1100π(cos(100π⋅1200)−cos(100π⋅0)))
Calculating the cosine values:
cos(100π⋅1200)=cos(π2)=0
cos(0)=1
Thus, we have:
Q=50(−1100π(0−1))=50(1100π)
Q=50100π=12π
To find the numerical value of Q:
Q≈12⋅3.14≈0.159Coulombs
The total charge that passes any point from t=0 to t=1200 seconds is approximately:
Q≈0.159C
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (Straight Objective Type Questions))
4 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Electric current through a conductor varies with time as I(t)=50sin(100πt). Here I is in amperes and t in seconds. Total charge that passes any point from t=0 to t=1200s is
View SolutionThe current in a 90mH inductor changes with time as i=1.0t2−6t, where I is in amperes and t is in seconds.
View SolutionThe current l through a given cross -section varies with time t as I=3+2t , where l is in ampere and t is in second. The charge passed through this cross-section dring t=0 to t=2 s is
View SolutionThe current through a wire depends on time as, i=(10+4t) Here , i is ampere and t in seconds. Find the charge crossed through section in time interval between t=0 to t=10s.
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe current in a conductor varies with time .t. as I=3t+4t2. Where I in amp and t in sec. The electric charge flows through the section of the conductor between t = 1s and t = 3s
View SolutionIn the circuit shown in figure q varies with time t as q=(16t2). Here q is in coulomb and t in second.

Find Vabatt=5s
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
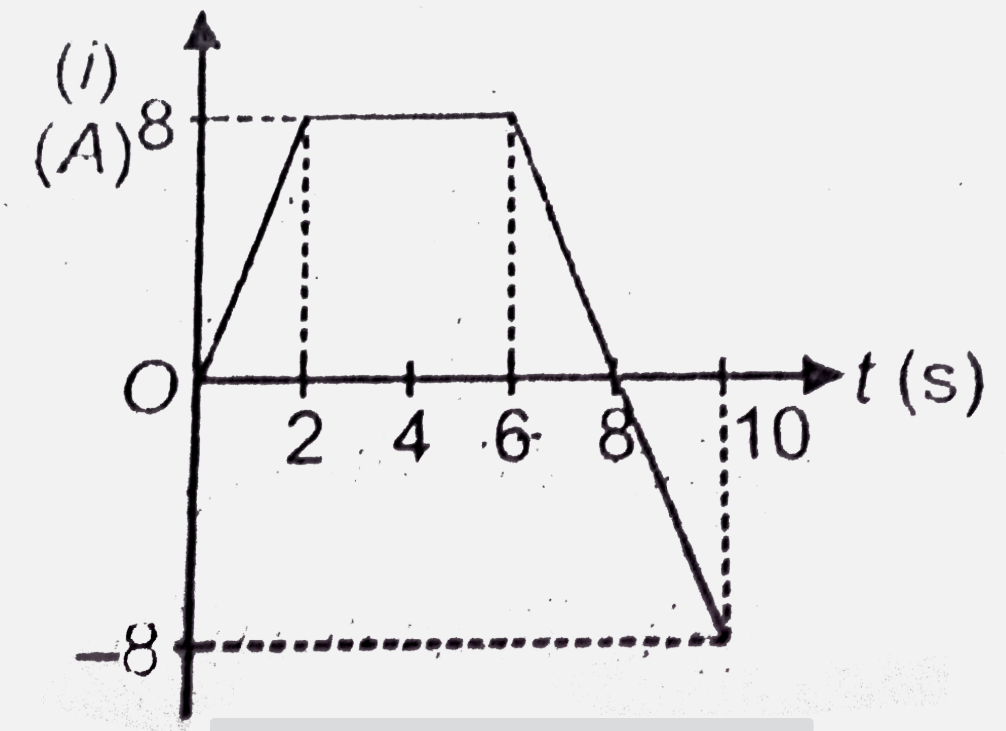
View SolutionThe current in a wire varies with time according to the equation I=4+2t. where I is in ampere and t is in second. Calculate the quantity of charge that passes through a cross section of the wire during the tiem t = 2s, to t=6s.
View Solution
