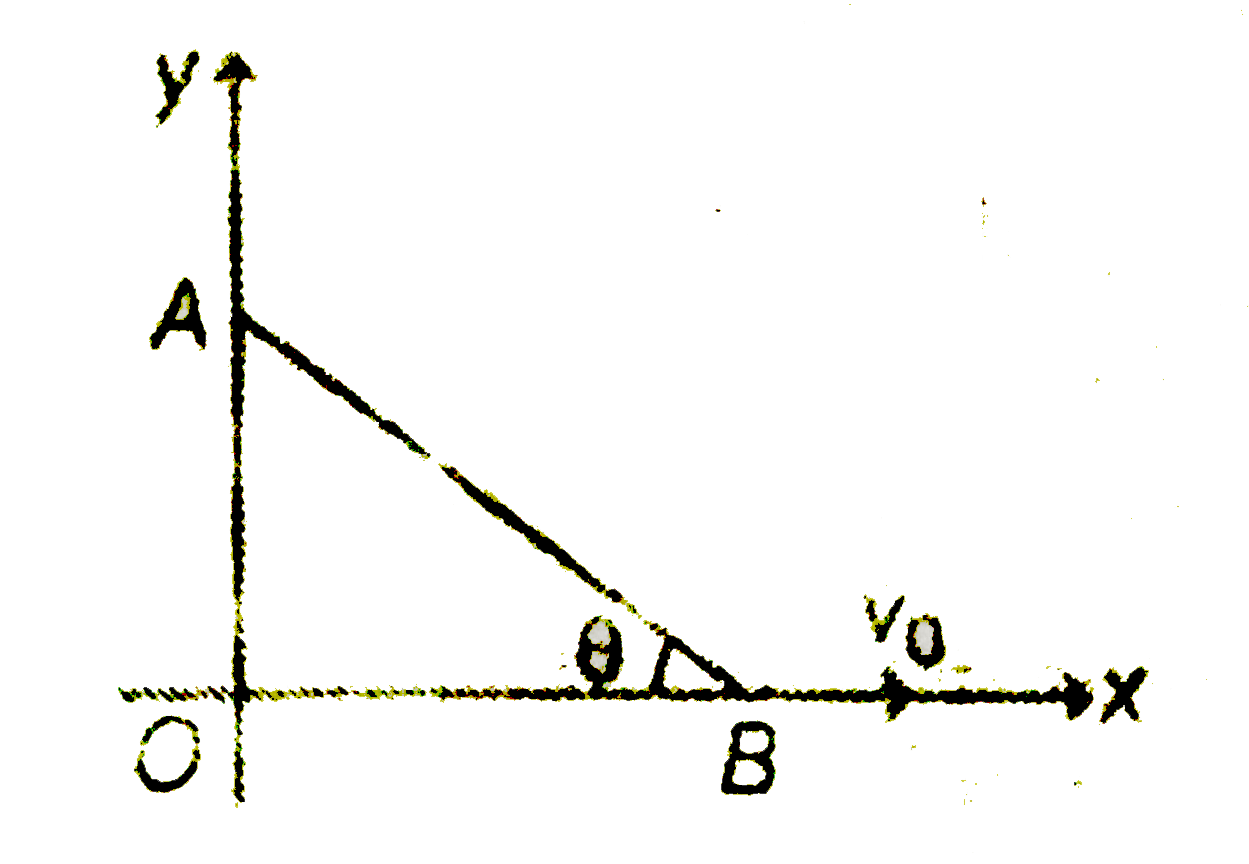
End A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rod
57v0 at tan−143 below horizontal
57v0 at tan−134 below horizontal
56v0 at tan−134 below horizontal
56v0 at tan−143 below horizontal
The correct Answer is:D
xCM=x2
⇒VCM=12dxdt0=v02(→)
⇒yCM=y2
yCM=12dydt=vB2=23v0⏐⏐
⏐↓
VCM=√v204+4v209=56v0 at tan−1(43) below horizontal
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘, the angular velocity of the rod is pqv0l. Find (p+q).
'(##CEN_KSR_PHY_JEE_C07_009_Q05##) '
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution
Knowledge Check
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
 Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant
Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant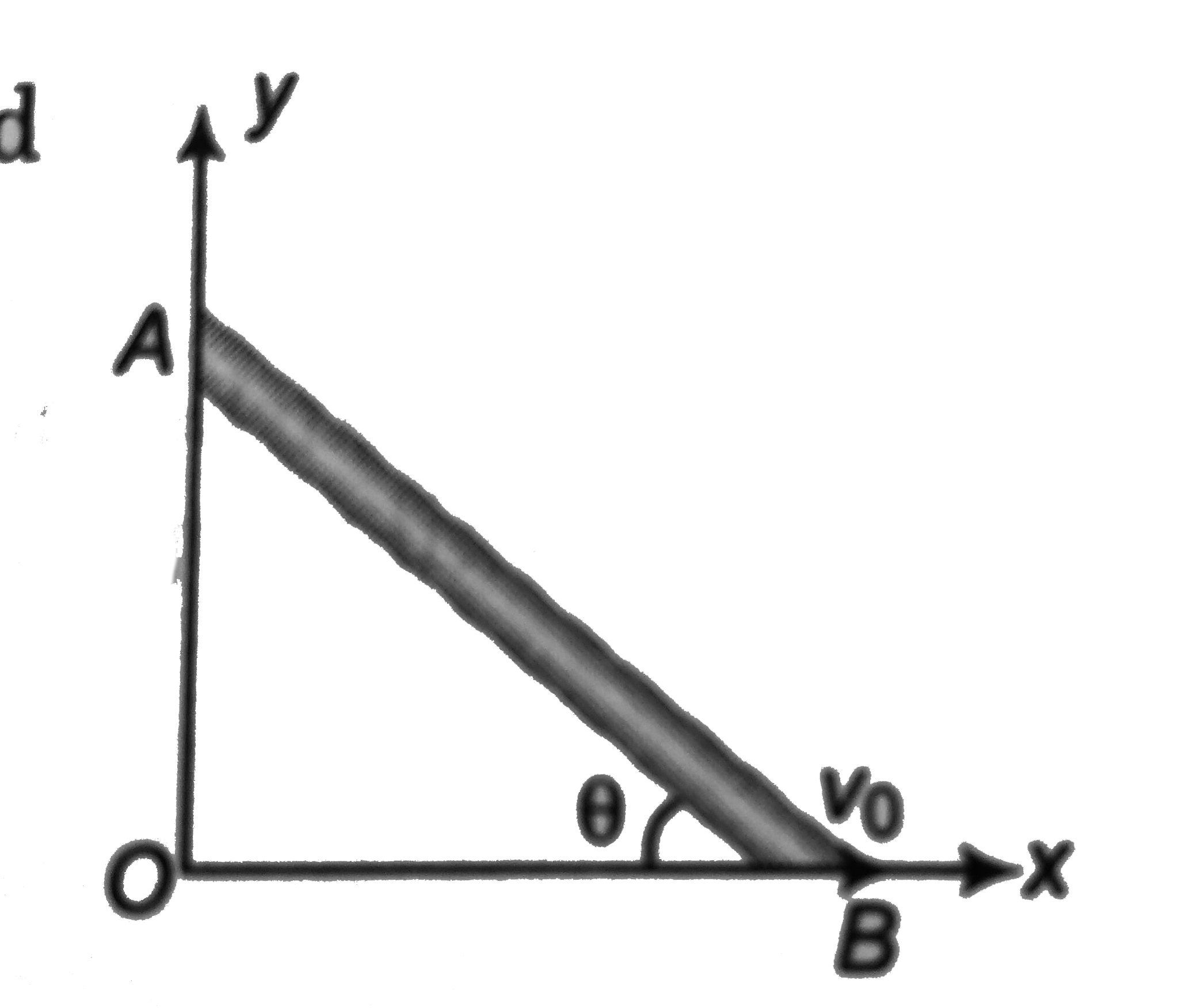
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.A rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
A2ms−1B1ms−1C4ms−1D1.5ms−1
A conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
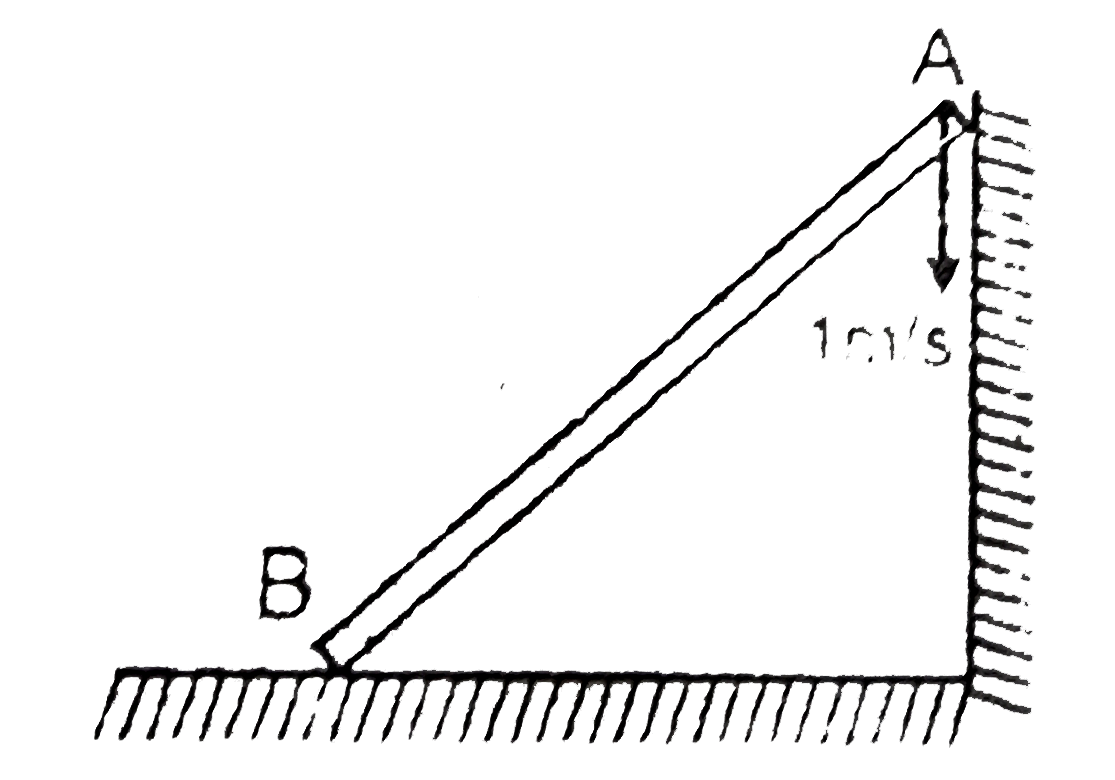
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :
View SolutionA disk is fixed at its centre O and rotating with constant angular velocity ω. There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30∘ with the vertical the ring is found to have a velocity v in the upward direction. Find ω of the disk. Given that the point A is R/2 distance above point O and length of the rod Ab is l
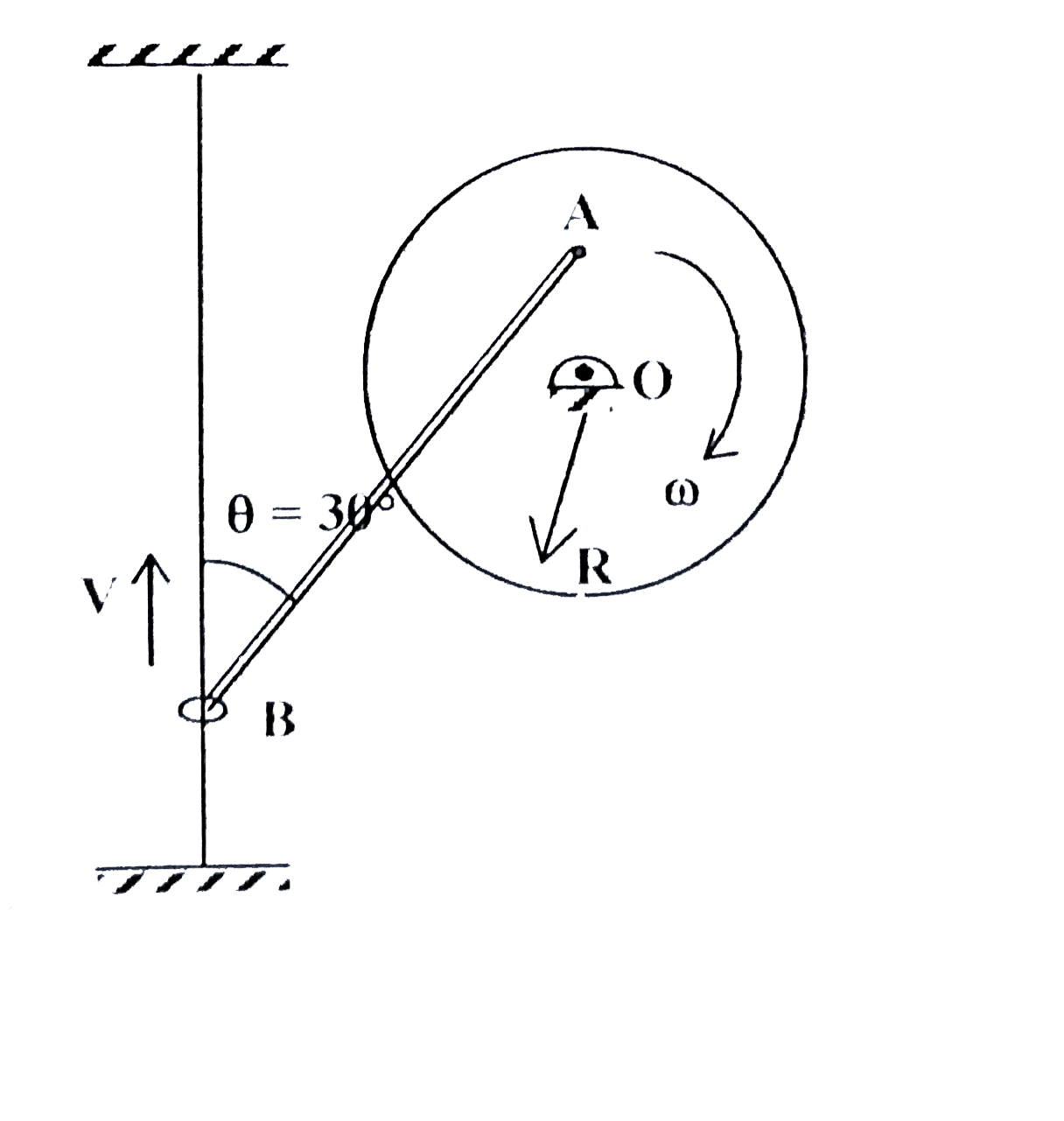
View Solution
