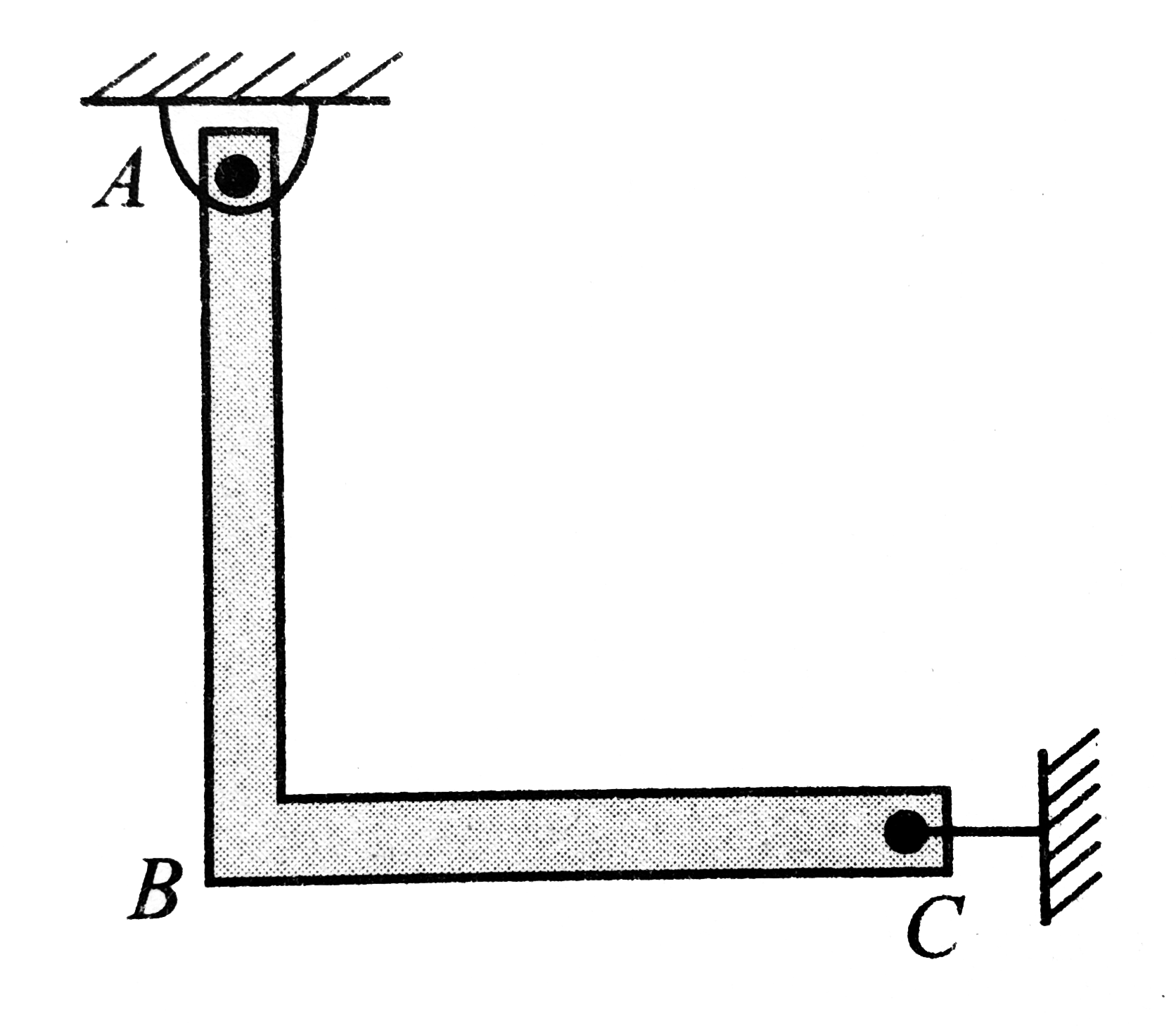
An $L$ shaped uniform rod of mass $2 M$ and length $2 L (A B = B C = L)$ is held as shown in Fig. with a string fixed between $C$ and wall so that $A B$ is vertical and $B C$ is horizontal. There is no friction between the hinge and the rod at $A$ .

If the string is burnt, find the angle between $A B$ and the vertical at equilibrium position.

A

${tan}^{- 1} (\frac{1}{3})$

B

${tan}^{- 1} (\frac{1}{4})$

C

${tan}^{- 1} (3)$

D

${tan}^{- (- 1)} (\frac{1}{2})$

Text Solution

Verified by Experts

The correct Answer is:A

$D$ is the $C M$ of the rod
In triangle $A D E$ :
$tan θ = \frac{L / 4}{3 L / 4}$
$\Rightarrow tan θ = \frac{1}{3} \Rightarrow θ = {tan}^{- 1} (1 / 3)$
here $D$ is the centre of mass. In equilibrim, $D$ will be vertically below $A$ . so i equilibrium $A B$ will make angle $θ$ as calculated above with the vertical.

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

An $L$ shaped uniform rod of mass $2 M$ and length $2 L (A B = B C = L)$ is held as shown in Fig. with a string fixed between $C$ and wall so that $A B$ is vertical and $B C$ is horizontal. There is no friction between the hinge and the rod at $A$ .

Find the tension in the string
A $\frac{M g}{3}$
B $\frac{M g}{4}$
C $M g$
D $\frac{M g}{2}$
An $L$ shaped uniform rod of mass $2 M$ and length $2 L (A B = B C = L)$ is held as shown in Fig. with a string fixed between $C$ and wall so that $A B$ is vertical and $B C$ is horizontal. There is no friction between the hinge and the rod at $A$ .
What will be the reaction between hinge and rod at point $A$ ?
A $\sqrt{65} \frac{M g}{4}$
B $2 M g$
C $\sqrt{17} \frac{M g}{4}$
D $\sqrt{17} \frac{M g}{2}$
A uniform L-shaped rod of mass 2m and length 2L, hangs from a hinge as shown (AO is horizontal and OB is vertical). If it is released from the position shown, then find the maximum angular velocity acquired by the end.

A $\sqrt{\frac{3 g}{l}}$
B $\sqrt{\frac{3 g}{l} (\sqrt{2} - 1)}$
C $\sqrt{\frac{3 g}{2 l} (\sqrt{2} - 1)}$
D $\sqrt{\frac{3 g}{2 l} (\sqrt{2} + 1)}$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Linked Comprehension

Home
Ask Doubt
Profile