Energy of a satellite going around the earth in an elliptical orbit is given by −GMm2a where M and m are masses of the earth and the satellite respectively and 2a is the major axis of the elliptical path. A satellite is launched tangentially with a speed √3GM5R from a height h = R above the surface of the earth. Calculate its maximum distance from the centre of the earth
The correct Answer is:2R
Step by step video, text & image solution for Energy of a satellite going around the earth in an elliptical orbit is given by -(GMm)/(2a) where M and m are masses of the earth and the satellite respectively and 2a is the major axis of the elliptical path. A satellite is launched tangentially with a speed sqrt((3GM)/(5R) from a height h = R above the surface of the earth. Calculate its maximum distance from the centre of the earth by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A satellite of mass m0 is revolving around the earth in circular orbit at a height of 3R from surface of the earth the areal velocity of satellite is (where R is radius of earth and M0 is the mass of earth)
View SolutionA satellite is launched tangentially from a height h above earth's surface as shown.
I. Find vmin so that it just touches the earth's surface
II. If h = R and satellite is launched tangentially with speed =√3GM5R
find the maximum distance of satellite from earth's centre .
View Solution
Knowledge Check
A satellite revolves around the earth in an elliptical orbit. Its speed is
Asame at all points on the orbit.Bgreatest when it farthest from the earthCgreatest when it is closest to the earthDgreatest neither when it is closest nor when it is farthest from the earth, but at some other point.A satellite revolves around the earth in elliptic orbit ,its speed is :
Asame at all points on the orbitBgreatest when its is farthest from the earthCgreatest when its is closest to the earthDNone of theseA geostationary satellite is at a height h above the surface of earth. If earth radius is R-
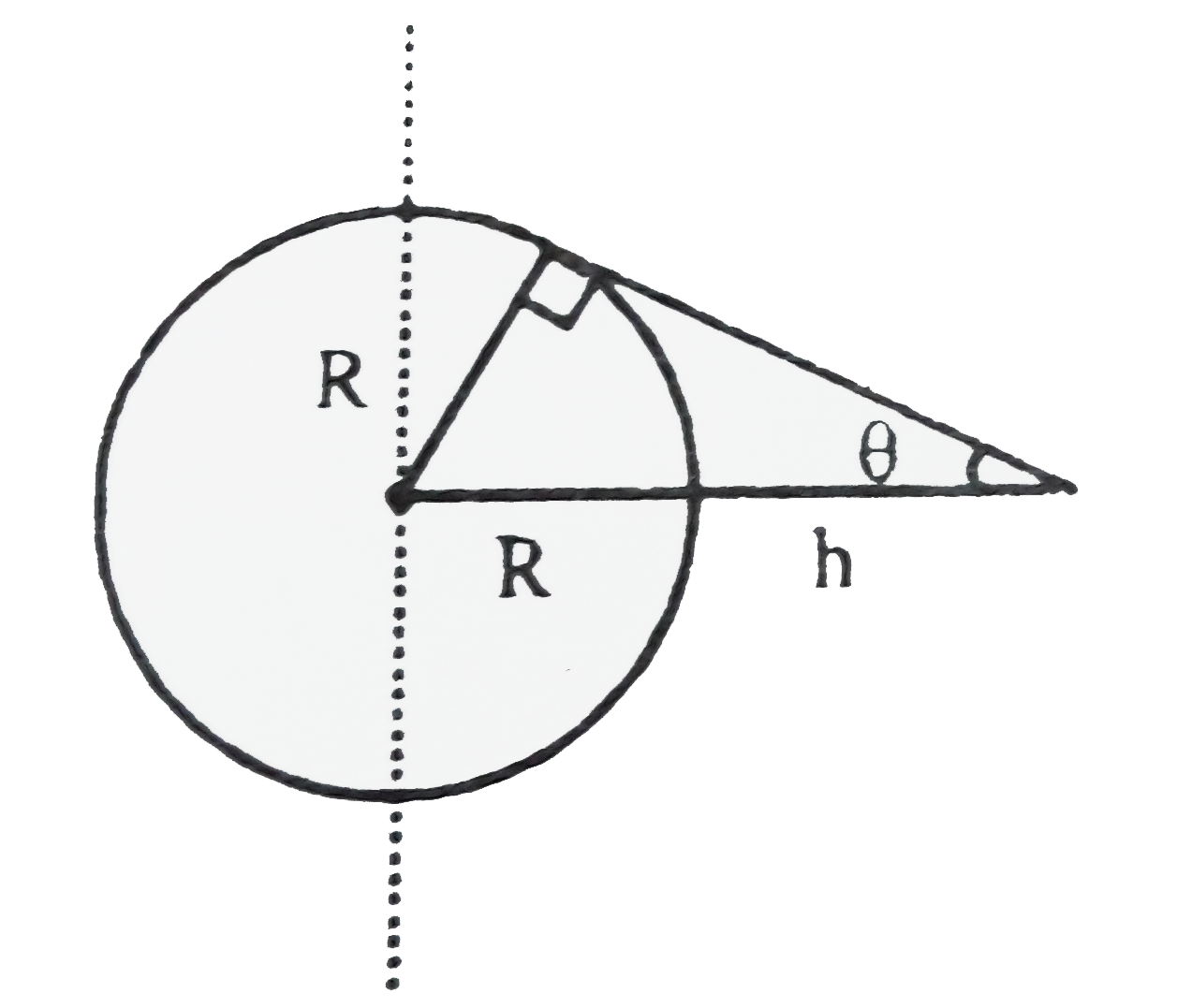 AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
The potential energy of a satellite of mass m revolving at height R above the surface of the earth where R= radius of earth is
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionA satellite of mass m orbits around the Earth of mas M in an elliptical orbit of semi - major and semi - minor axes 2a and a respectively. The angular momentum of the satellite about the centre of the Earth is
View SolutionA satellite of mass m is Launched from the earth's surface in a circular orbit. If M and R denote the mas and radius of the earth respectively, then the total energy of the satellite at an altitude 2R is
View SolutionAn artificial satellite is placed into a circular orbit around earth at such a height that it always remains above a definite place on the surface of earth. Its height from the surface of earth is
View Solution
