Example why:
(i) we slip when step on a banana pell.
(ii) lubricants are used in matchines.
(iii) a hover-creft travels much faster then a steamer pushing through water.
(iv) aeroplanes, missiles, and space ships have their front pointed.
(i)The banana peel breaks the interlocking between our feet and ground.
(ii)The lubricant fills the fine pores or depressions in the surfaces.
(iii)Friction offered by water is more.
(iv) At the pointed ends the surface area is less.
Topper's Solved these Questions
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE.
1 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)
3 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
1 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
Similar Questions
Give reasons for the following :
(i) Molecular mass of ethanol and dimethyl ether is the same, however ethanol is a liquid at room temperature but dimethyl ether is a gas.
(ii) Anhydrous CaCl2 cannot be used for drying ethanol
(iii) tertiary Alcohols form the turbidity fastest in Lucas test while primary alcohols form slowest.
(iv) Ethyl alcohol reacts with HI but not with HCN.
(v) Sodium metal can be used for drying diethyl ether but not ethanol.
(vi) Propanol, unlike propane is soluble in water.
(vii) Propanol boils at a higher temperature than propane.
(viii) Why glycerol has high viscosity and is miscible with water in all proportions ?
(ix) Reactivity of HX with alcohols is in the order, HI>HBr>CHl>HF
(x) Why is it not posssible to obtain a halide by reacting ROH with X− ?
(xi) ClCH2CH2OH is stronger acid than CH3CH2OH.
(xii) Hydration of 3-phenylbut-1-ene in dil. H2SO4 forms 2-phenylbutan-2-ol instead of 3-phenylbutan-2-ol.
(xiii) The compound (CH(3))2C−CH(OH)CH3 on treatment with conc. HCl forms (CH3)2C(Cl)−CH(CH3)2 instead of (CH3)3C−CH(Cl)CH3
(xiv) Acid catalysed dehydration of t-butanol is faster than that of n-butanol.
(xv) When t-butanol and n-butanol are separately treated with a few drops of dilute KMnO4, in one case only, the purple colour disappears and a brown precipitate is formed. Which of the two alcohols gives the above reaction and what is brown precipitate ?
View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision

View Solution
Knowledge Check
In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QThe graph shows the psition of a hard ball with respect to time .The hard ball hits and rebounds on the hard surface .Ehich of the following graph represent the correct variation with repect to time?
 A
A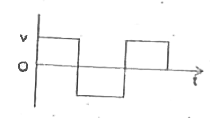 B
B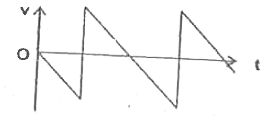 C
C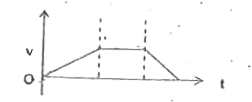 Dnone of these
Dnone of theseIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision
 AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth l
AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth lWhen a current through the medium, an electric field exists as well as a potential which varies in space. Suppose that there is a break in a high - voltage transmission line and the free end of a wire of length L is lying on the ground. An electric current flows through the regions of soil adjoining the conductor. If a man happens to be walking near by a potential difference, which is called the step voltage appears between the points where his feet touch the ground, Consequently, an electric current whose strength depends on this potential difference flows through the man.
Let us calculate the step voltage. Since the conductor is quite long, we assume that the current flows from it to the ground in a direction perpendicular to the conductor. The equipotential surfaces are the surfaces of semi-cylinders whose axes coincide with the conductor. Suppose that the man is walking in a direction perpendicular to the conductor with a step of length 'b' the distance between the conductor and the foot closer to it being d. Assuming that the current flows uniformly from the conductor over the semi cylindrical region we obtain the following expression for the current density at a distance from the conductor:
j=iπrL
In this case , the field strength along the radii perpendicular to the conductor is Er=jσ=lπrLσ
Consequently , the step voltage is Vst=∫d+bdEdr=1πσLln(d+bd)
For example , If l=500A , d=1 m , b=65 cm and L=30 m we find that Vst=270 V. Much higher voltages may appear under other conditions and other shapes of conductors.
When a part of a high- voltage transmission line falls on the ground, it creates a hazardAbecause there can be a direct contact between the cable and a human beingBbecause of the emergence of step voltages.Cboth (A) and (B)Dnone of (A) and (B)
Read the following passage carefully and answer the questions:
ASEAN was and still remains principally an economic association, While the ASEAN region as a whole is a much smaller economy campared to the US the EU, and Japan, its economy is growing much faster than all these. This accounts for the growth in its influence both in the region and beyond. The objectives of the ASEAN Economic Community are to create a common market and production base within ASEAN States and to aid social and economic development in the region. The Economic Community would also like to improve the existing ASEAN Diputes Settlement Mechanism to resolve economic diputes. ASEAN focused on creating a Free Trade Area (FTA) for investment, labour and services. The US and China have already moved fast to negotiata FTAs with ASEAN.
(i) What is the objective of ASEAN Economic Community?
(ii) Why did ASEAN establish Free Trade Areas (FTAs) ?
(iii) How ASEAN Economic Community would resolve economic disputes?
(iv) Which countries have already moved fast to negotiate FTAs with ASEAN and why?
View SolutionAccount for the following :
(i) Ethers have significant dipole moments.
(ii) Ethers have lower boiling points than the corresponding isomeric alcohols but approximately equal to a paraffin with similar molecular mass structure.
(iii) HI is better reagent than HBr for cleavage of ethers.
(iv) Why a non-symmetrical ether is not prepared by heating a mixture of ROH and R'OH in acid ?
(v) Why is it possible to prepare tertiary butyl ethyl ether in good yield by heating tertiar butanol and ethanol ?
(vi) Ether are soluble in conc. H2SO94) but ethers separate out from the solution on addition of water.
(vii) Why id diethyl ether used as a solvent for (i) BF3 and (ii) RMgBr ?
(viii) Sometimes explosion occrs during distillation of an ether sample.
(ix) Why [(CH3)3C]2O cannot be prepared either by Williamson's reaction or by dehydration of tertiary butyalcohol ?
(x) Why ArO-R ethers are clearved with HI to give RI and ArOH rather than ArI and R-OH ?
(xi) Which of the following is the correct method for synthesising methyl tert-butyl ether and why ?
(a) (CH3)3C−Br+NaOMe→
(b)CH3+NaO−T−Bu→
(xii) 2,2-Dimethyl oxirane can be cleaved by acid (H+) . Write mechanism.
(xiii) Write the equations of the reaction of hydrogen iodide with :
(i) 1-Propoxypropane (ii) Methyoxybenzene
9iii) Benzyl ethyl ether
View SolutionRead the passage carefully and select the best answer to question out of the given four alternatives.
PASSAGE - III
Let.s move to the crackling topic of the SC.s firecracker ban in Delhi. Like me and millions of other children raised in India, Masaba must have celebrated Diwali with new clothes, sweets and the quintessential rockets, anars and phuljharis. But when she supports the ban on firecrackers because of the pollution it creates, the earthworms once again flail desperately, not by quoting statistics or making logical arguments to refute her point but by muckraking. .Don.t mess with our ancient traditions,. they say. I would like to tell them that if we stuck to all our traditions just because they.re ancient then we should still be pushing widows into funeral pyres to commit sati and get our children married off at the age of eight.
As much as I would like to see the delight on my daughter.s face - the same glee I had as a child - while bursting atom bombs and laris, it is the present scenario and not nostalgia that must dictate my actions. If even doctors welcome the ban as they feel fumes from firecrackers take pollution levels beyond safe limits, then perhaps we need to change our traditional values and create new ones. If saying that makes me a bad Indian, then so be it.
One of the greatest privileges I have - in fact because of the very background that they are trying to smear - stems from the fact that I was lucky enough to have a mother who has raised me to believe that equality isn.t one of my privileges but it is my right. One that was hard won by some brave and fearless women, women who set the right precedent for other women by standing against inequality.
The flailing trollers do not realize that you cannot shame us by pulling down our mothers, those fiercely independent women who have lived life on their own terms, who have not just talked the talk but walked the walk. Yes, you can reason with us by presenting a logical argument but this ems to be beyond the resources of these anonymous creatures hiding their faces in the mud.
And yes one last thing, for all those claiming to be the flag - bearers of ancient traditions, it would be lovely if you adhered to your so -called traditional ways completely. Why do you write open letters, tweet and troll in the language of the Brits? Why not go traditional there as well, use only our ancient languages and spare us your venom-filled and grammatically incorrect English?
Who do you think is the author of the passage?
View SolutionRead the passage carefully and select the best answer to question out of the given four alternatives.
PASSAGE - III
Let.s move to the crackling topic of the SC.s firecracker ban in Delhi. Like me and millions of other children raised in India, Masaba must have celebrated Diwali with new clothes, sweets and the quintessential rockets, anars and phuljharis. But when she supports the ban on firecrackers because of the pollution it creates, the earthworms once again flail desperately, not by quoting statistics or making logical arguments to refute her point but by muckraking. .Don.t mess with our ancient traditions,. they say. I would like to tell them that if we stuck to all our traditions just because they.re ancient then we should still be pushing widows into funeral pyres to commit sati and get our children married off at the age of eight.
As much as I would like to see the delight on my daughter.s face - the same glee I had as a child - while bursting atom bombs and laris, it is the present scenario and not nostalgia that must dictate my actions. If even doctors welcome the ban as they feel fumes from firecrackers take pollution levels beyond safe limits, then perhaps we need to change our traditional values and create new ones. If saying that makes me a bad Indian, then so be it.
One of the greatest privileges I have - in fact because of the very background that they are trying to smear - stems from the fact that I was lucky enough to have a mother who has raised me to believe that equality isn.t one of my privileges but it is my right. One that was hard won by some brave and fearless women, women who set the right precedent for other women by standing against inequality.
The flailing trollers do not realize that you cannot shame us by pulling down our mothers, those fiercely independent women who have lived life on their own terms, who have not just talked the talk but walked the walk. Yes, you can reason with us by presenting a logical argument but this ems to be beyond the resources of these anonymous creatures hiding their faces in the mud.
And yes one last thing, for all those claiming to be the flag - bearers of ancient traditions, it would be lovely if you adhered to your so -called traditional ways completely. Why do you write open letters, tweet and troll in the language of the Brits? Why not go traditional there as well, use only our ancient languages and spare us your venom-filled and grammatically incorrect English?
What do you infer by the term "not just talked the talk but walked the walk"?
View SolutionRead the passage carefully and select the best answer to question out of the given four alternatives.
PASSAGE - III
Let.s move to the crackling topic of the SC.s firecracker ban in Delhi. Like me and millions of other children raised in India, Masaba must have celebrated Diwali with new clothes, sweets and the quintessential rockets, anars and phuljharis. But when she supports the ban on firecrackers because of the pollution it creates, the earthworms once again flail desperately, not by quoting statistics or making logical arguments to refute her point but by muckraking. .Don.t mess with our ancient traditions,. they say. I would like to tell them that if we stuck to all our traditions just because they.re ancient then we should still be pushing widows into funeral pyres to commit sati and get our children married off at the age of eight.
As much as I would like to see the delight on my daughter.s face - the same glee I had as a child - while bursting atom bombs and laris, it is the present scenario and not nostalgia that must dictate my actions. If even doctors welcome the ban as they feel fumes from firecrackers take pollution levels beyond safe limits, then perhaps we need to change our traditional values and create new ones. If saying that makes me a bad Indian, then so be it.
One of the greatest privileges I have - in fact because of the very background that they are trying to smear - stems from the fact that I was lucky enough to have a mother who has raised me to believe that equality isn.t one of my privileges but it is my right. One that was hard won by some brave and fearless women, women who set the right precedent for other women by standing against inequality.
The flailing trollers do not realize that you cannot shame us by pulling down our mothers, those fiercely independent women who have lived life on their own terms, who have not just talked the talk but walked the walk. Yes, you can reason with us by presenting a logical argument but this ems to be beyond the resources of these anonymous creatures hiding their faces in the mud.
And yes one last thing, for all those claiming to be the flag - bearers of ancient traditions, it would be lovely if you adhered to your so -called traditional ways completely. Why do you write open letters, tweet and troll in the language of the Brits? Why not go traditional there as well, use only our ancient languages and spare us your venom-filled and grammatically incorrect English?
According to the passage why do the doctors welcome the ban?
View Solution
