The ratio of $μ_{k}$ (kinetic friction) and $μ_{s}$ (state friction) is

greater than 1

less than 1

equal to 1

depends on condition

Text Solution

Verified by Experts

The correct Answer is:b

Updated on:21/07/2023

A block of mass M is sliding down the plane. Coefficient of static friction is $μ_{s}$ and kinetic friction is $μ_{k}$ . Then friction force acting on the block is :

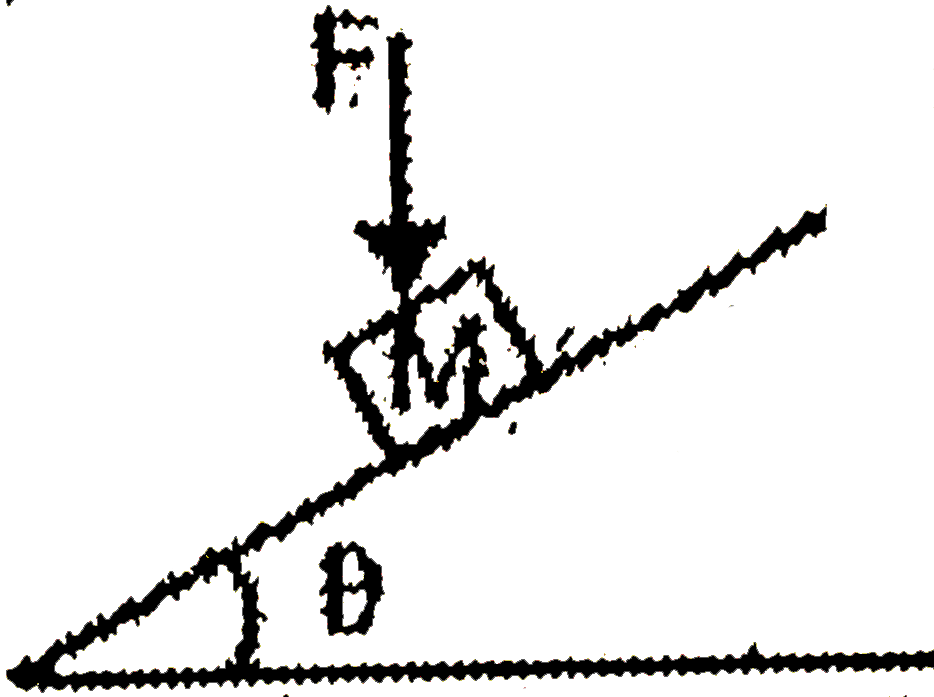A $(F + M g) sin θ$
B $μ_{k} (F + M g) cos θ$
C $μ_{s} M g cos θ$
D $(M g + F) sin θ$
Which is true for rolling friction $(μ_{r})$ , static friction $(μ_{s})$ and kinetic friction $(μ_{k})$ ?
A $μ_{s} > μ_{k} > μ_{r}$
B $μ_{s} < μ_{k} < μ_{r}$
C $μ_{s} < μ_{k} > μ_{r}$
D $μ_{s} > μ_{k} > μ_{r}$
If coefficient of static friction is $μ_{s}$ and coefficient of kinetic friction is $μ_{k}$ , which one is correct ?
A $μ_{s} = μ_{k}$
B $μ_{s} > μ_{k}$
C $μ_{s} < μ_{k}$
D $μ_{s} \leq μ_{k}$