Question

Explain by plats the position of particle executing simple harmonic motion at different time.

Explanation

The figure shows the positions of a particle executing S.H.M. are at discrete value to time, each interval of time being `(T)/(4)" where "phi = 0` and T is the period of motion.

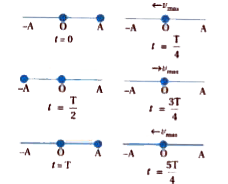
For a given SHM, A is the amplitude, then the velocity and position of a particle at time t is determine by the phase `(omega t+ phi)` of cosine function.
In the equation of SHM `x(t) = A cos (omega t+phi), phi =0" and " omega = (2pi)/(T)`,
`x(t)= A cos ((2pi)/(T)t)`
Now `t=0`
`x(t)= A cos (0) = +A`
Taking `t=(T)/(4)`
`x(t)= A cos"" ((2pi)/(T)xx(T)/(4)) = Acos ""(pi/2)= 0`
Taking `t=(T)/(2)`
`x(t)= A cos ""((2pi)/(T)xx(T)/(2)) = Acos ""pi = -A`
Taking `t=(3T)/(4)`
`x(t)= A cos ""((2pi)/(T)xx(3T)/(4)) = Acos ""(3pi)/(2)= 0`
Taking `t=T`
`x(t)= A cos ""((2pi)/(T)xxT) = Acos ""2pi = +A`
Taking `t=(5T)/(4)`
`x(t)= A cos ""((2pi)/(T)xx(5T)/(4)) = Acos ""(5pi)/(2)= 0`
From figure got following observations :
(i) After period T, periodic (repeats) motion takes place.
(ii) Period T remains fixed no matter what location you choose as the initial (t=0) location.
(iii) The speed is maximum for zero displacement (at x=0) and zero at the extremes of motion (x= A).