Question

Explain clearly, with examples, the difference between :
(a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of the path covered by a particle over the same interval;
(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first.
When is the equality sing true? [ For simplicity, consider one- dimensional motion only]

Explanation

(a) The magnitude of displacement over an interval of time is the shortest distance (which is a straight line) between the initial and final positions of the particle.
The total path length of a particle is the actual path length covered by the particle in a given interval of time.
For example, suppose a particle moves from point A to point B and then, comes back to a point, C taking a total time t, as shown below. Then, the magnitude of displacement of the particle = AC.

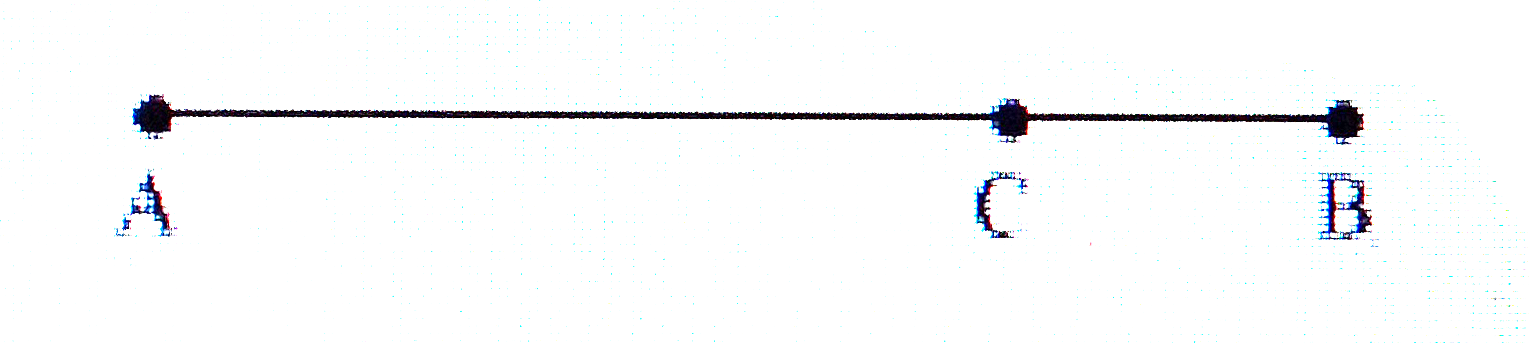
Whereas, total path length = AB + BC
It is also important to note that the magnitude of displacement can never be greater than the total path length. However, in some cases, both quantities are equal to each other.
(b)Magnitude of average velocity =`("Magnitude of displacement")/("Time interval")`
For the given particle,
Average velocity =`(AC)/t`
Average speed =`("Total path length")/("Time interval")`
`=(AB+BC)/t`
Since (AB + BC) gt AC, average speed is greater than the magnitude of average velocity. The two quantities will be equal if the particle continues to move along a straight line.