Explain clearly, with ezamples, the difference between :
(a) magnitude of displacemnt (sometimes called distance ) overand
interval of time, and the total length of the path coverd by a particle over the same interval.
(b) magnitude of average velocity over an intercal of time , and the average speed
over the same interval. [ Average speed of a particle over an interval of time is defined as the toal path length
divided by the time intrval]. Show in both (a) and (b) that the second quantity is either greater than or equal to first.
When is the equality sing true ? [ For simplocity, consider one- dimensional motion only]
(a) The magnitude of displacement over an interval of time is the shortest distance (which is a straight line) between the initial and final positions of the particle.
The total path length of a particle is the actual path length covered by the particle in a given interval of time.
For example, suppose a particle moves from point A to point B and then, comes back to a point, C taking a total time t, as shown below. Then, the magnitude of displacement of the particle = AC.
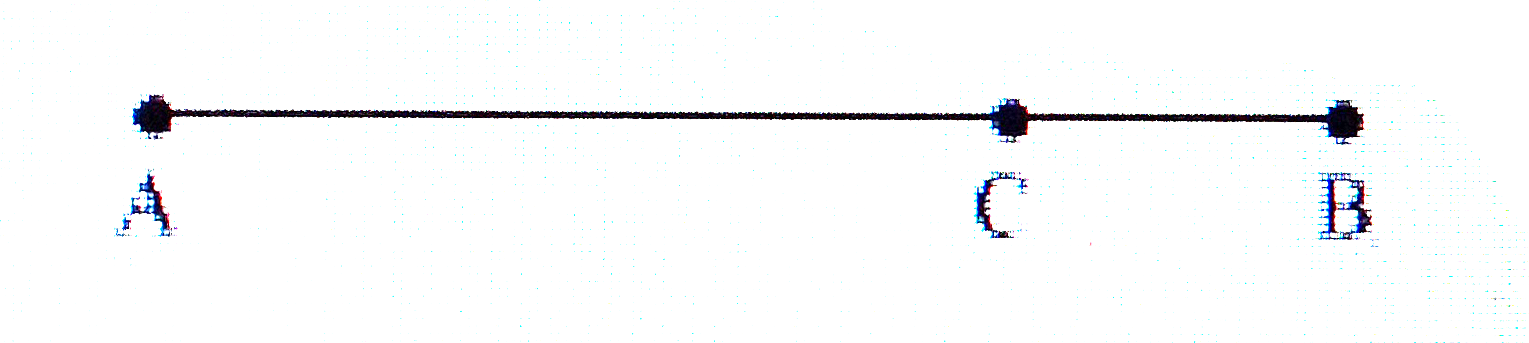
Whereas, total path length = AB + BC
It is also important to note that the magnitude of displacement can never be greater than the total path length. However, in some cases, both quantities are equal to each other.
(b)Magnitude of average velocity =Magnitude of displacementTime interval
For the given particle,
Average velocity =ACt
Average speed =Total path lengthTime interval
=AB+BCt
Since (AB + BC) gt AC, average speed is greater than the magnitude of average velocity. The two quantities will be equal if the particle continues to move along a straight line.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area under velocity-time graph for a particle in a given interval of time represnets
AvelocityBaccelerationCwork doneDDisplacement does not tell the nature of the actual motion of a particle between the points.
If magnitude of average speed and average velocity over a time interval are same, then
View SolutionUnder what condition is the magnitude of the average velocity of a particle moving in onbe dimension smaller than the average speed over same time interval?
View SolutionA : The magntidue of average velocity in an interval can never be greater than average speed in that interval.
R : For a moving object distance traveled ≥|Displacement|
View SolutionAssertion: The magnitude of average velocity of the object over an interval of time is either smaller than or equal to the average speed of the object over the same interval.
Reason: Path length (distance) is either equal or greater than the magnitude of displacement.
View SolutionAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.
View SolutionCan the instantaneous velocity of an object during a time interval ever be greater in magnitude than average celocity over the entire interval ? Can it be less?
View SolutionA point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
View Solution
