Question

Explain in detail the triangle law of addition.

Explanation

Let us consider two vectors `vec A` and `vec B` as shown in figure. To find the resultant of the two vectors we apply the triangular law of addition as follows

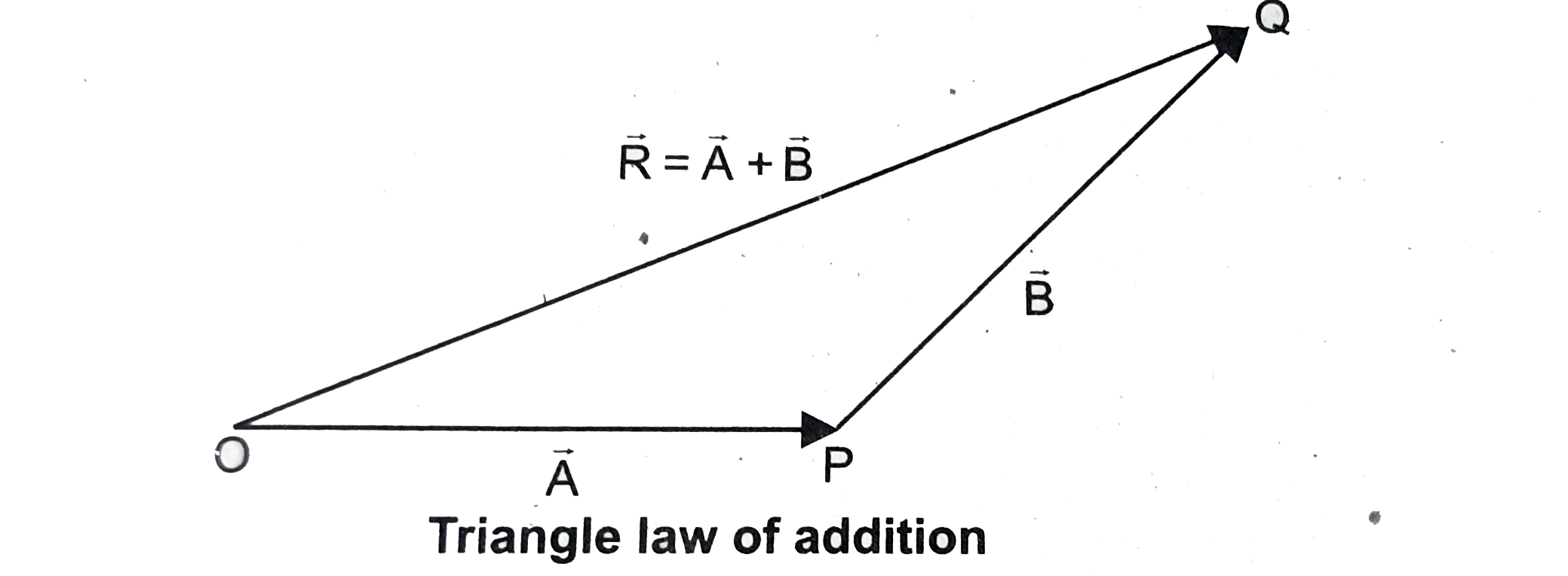
Represent the vectors `vec A` and `vec B` by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure To explain further, the head of the first vector `vec A` is connected to the tail of the second vector `vec B`. Let `theta` be the angle between `vec A` and `vec B` . Then `vec R` is the resultant vector connecting the tail of the first vector `vec A` to the head of the second vector `vec B`. The magnitude of `vec R` (resultant) is given geometrically by the length of `vec R` (OQ) and the direction of the resultant vector is the angle between R and Thus we write `vec R= vec A+ vecB`
`vec( OQ)= vec(OP) + vec( PQ)`
1. Magnitude of resultant vector: The magnitude and angle of the resultant vector are determined by using triangle law of vectors as follows. From figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle

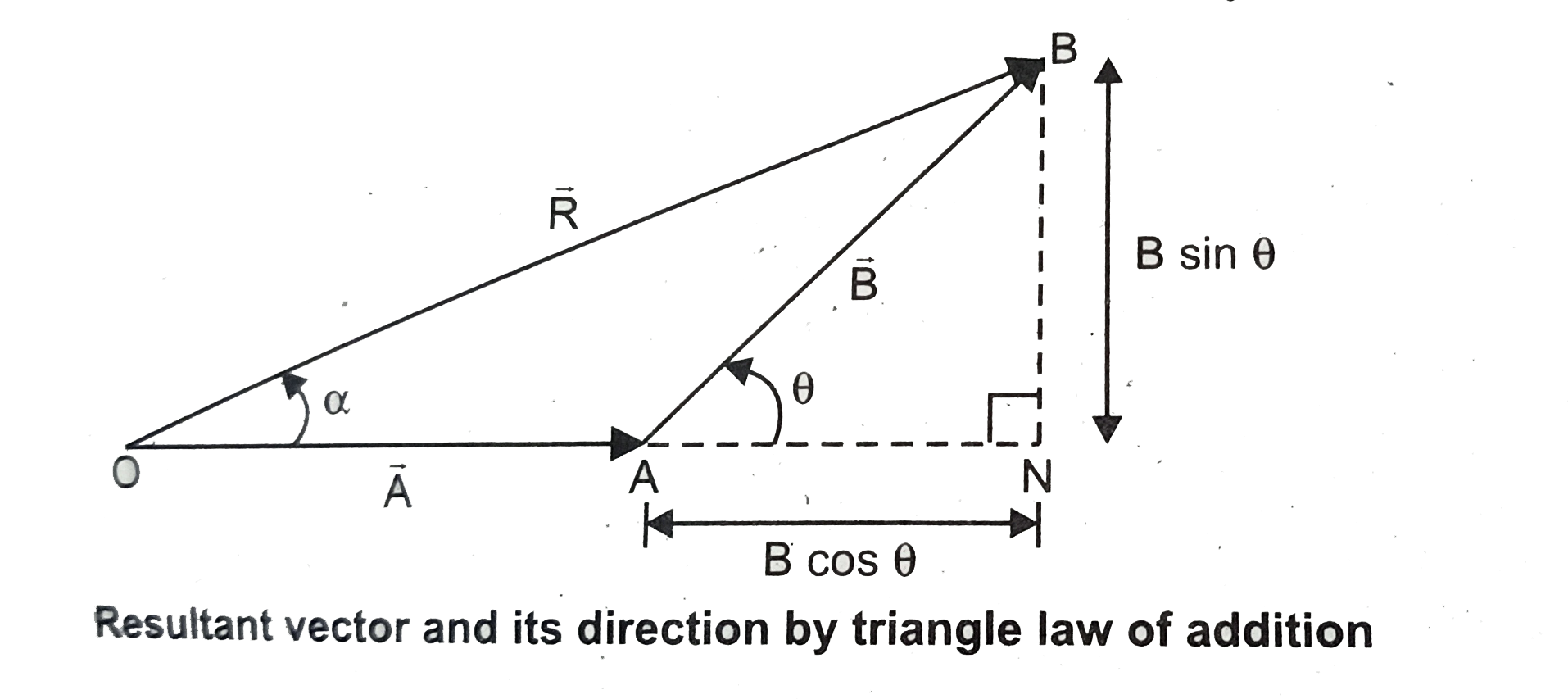
From figure, let R is the magnitude of the resultant of `vec A` and `vec B`.
`cos theta= (AN)/(B) therefore AN= Bcostheta and sintheta= (BN)/(B)`
`therfore BN= Bsin theta`
for Delta OBN , we have `OB^(2)= ON^(2)+ BN^(2)`
`implies R^(2)= (A+Bcostheta)^(2)+ (bsintheta)^(2)`
`implies R^(2)= A^(2)+ B^(2)cos^(2)theta+ 2ABcostheta+ B^(2)sin^(2)theta`
`implies R^(2)= A^(2)+ B^(2)(cos^(2)theta+ sin^(2)theta)+ 2ABcostheta`
`implies R^(2)= sqrt( A^(2)+ B^(2)+ 2ABcostheta)`
Direction of resultant vectors: If `theta` is the angle between `vec A` and `vec B`, then
`|vec A+ vec B|= sqrt( A^(2)+ B^(2)+ 2ABcostheta)`
If `vec R` makes angle `alpha` with A, then in `Delta`OBN,
`tan alpha =(BN)/(ON)= (BN)/(OA+AN)`
`tan alpha =(Bsintheta)/(A+Bcostheta)implies alpha = tan^(-1)((Bsintheta)/(A+Bcostheta))`