Question

Explain the parallel combination of resistors and derive the formula of equivalent resistance.

Explanation

Two or more than two resistors are said to be connected in parallel if one end of each resistor is connected to one point and the other end is connected to another point so that more than one paths are available for the current to flow and potential difference across each resistor is the same and is equal to the applied potential difference between the two common points.
Three resistors with resistances, `R_1, R_2 and R_3` are connected in parallel between points A and B as shown in the figure 12.16 (a).
Here. the current I gets divided at point A amongst three resistors as shown in the figure.
The value of the current flowing through each . resistor depends on the value of its resistance.

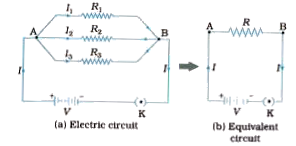
Let`I_1, I_2 and I_3` be the currents flowing through the resistors with resistances `R_1, R_2 and R_3` respectively.
`:. I =I_1 +I_2 + I_3` ... ... (12.12)
In a parallel combination of resistors, the potential difference across every resistor is equal < to the potential difference V of the battery. According to Ohm.s law,
`I_1 = V/R_1 ,I_2 = V/R_2 and I_3 = V/R_3`
`:. I_1 = V /R_1 + V/R_2 + V/R_3.......(12.13)`
Now, if a resistor with resistance `R_p`, instead of three resistors with resistances `R_1, R_2 and R_3`, is connected in the circuit such that the current flowing through the circuit remains the same as I then `R_p` is called the eqUivalent resistance of the circuit [see figure (b)).
`I = V/R_p` ......(12.14)
From equation (12.13).
`V/R_p =V/R_1 +V/R_2 + V/R_3`
`:. 1/(R_p)= 1/(R_1) + 1/R_2 + 1/R_3`
Thus, in a parallel combination of resistors, the sum of the reciprocals of the individual resistances is equal to the reciprocal of the eqUivalent resistance `R_p.R_p` is less than any of ? the individual resistances in the circuit.