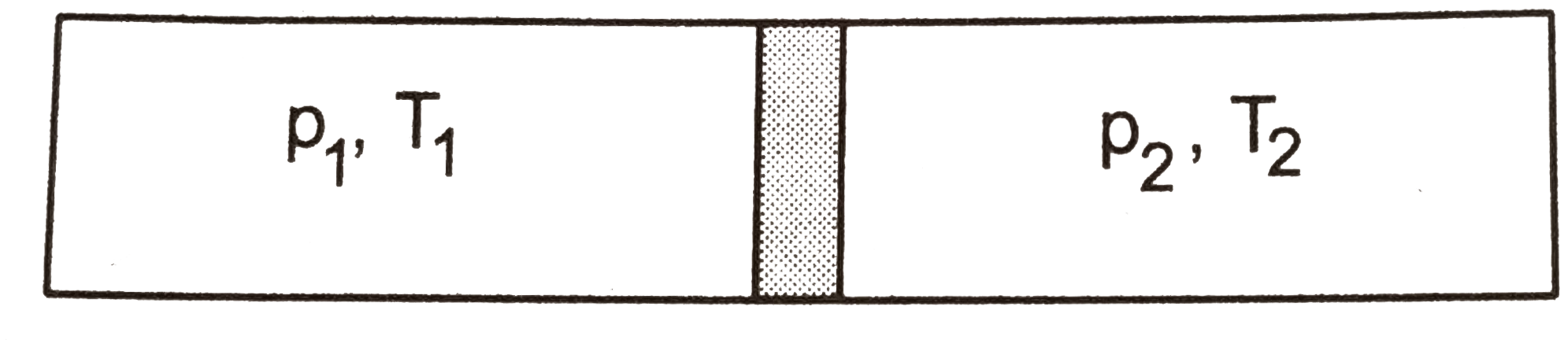
Fig shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the temperature becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium temperature. (d) how much heat has flown from the gas on the right to the gas on the left ?
The correct Answer is:A, B, C, D
(a) Since the wall cannt be moved<br>thus, Delta U = 0<br>and Delta Q = 0<br>hence, Delta D = 0<br>(b)Let final pressure in LTS =p1tˆ∈RHS=p2<br>SinceN⊙ofmo≤srema∈sconstant.
Sop1V2RT1=p2V2RT
⇒p1=p1T1
= (p_1T_1T_2(P_1+P_2)/(T_1lambda) AsT=T2T1(P1+P2)λ
p1T2(P1+P2)λ
SimilarlyP_2 = (p_2T_2(P_1+P_2))/(lambda)<br>(c)LetT2>T1and'T'be the common temperature
Initialy P−2v)2=n2RT1
⇒n1=P1V2RT1
HenseΔQ=0,ΔW=0
HenseΔU=0
∈caseLHS,Delta U_1 = 1.5n_2R(T-T_2)<br>in case LHS<br> = Delta U _2 = 1.5n_2R(T_2-T)<br>But Delta U_1-Delta U_2 = 0<br>rArr 1.5n_1R(T-T_1) =1.5n_2R(T_2-T) <br>rArr n_1T-n_1T_1 = n_2T_2-n_2T<br>rArrT(n_1+n_2) =n_1T_2+n_2T_2<br>rArr T = ( n_1T_1+n_2T_2)/(n_1+n_2)<br> = (P_1VxxT_1)/(2RT_1)+(P_2VxxT_2)/((2RT_2)/(P_1V)/(2RT_1)+(P_2V)/(2RT_1)<br> = ((P_1+P_2)T_1T_2)/(lambda)<br>as P_1T_2+P_2 = T_1lambda<br>(b)For RHS<br> Delta Q = Delta U = (asDelta W = 0)<br>1.5 n_2R(T_(2 )-T)<br> = (1.5 P_(2)V)/(2RT_(2)) R [T_(2) -((P_(1)+P_(2))T_(1)T_(2))/(P_(1)T_(2)+P_2T_(1))]<br> = (1.5P_(2)V)/(2RT_(2))xx(P_(1)T_(2)^2-P_(1)T_(1)T_(2))/(lambda)<br> = (1.5 P_(2) V)/(2RT_(2)) xx (T_(2) -P_(1) (T_(2)-T_(1)) / (lambda)<br> =(3P_(2)P_(1)V(T_(2)-T_(1)))/(4lambda)

Topper's Solved these Questions
Similar Questions
A cylindrical tube with adiabatic walls having volume 2V0contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are P0,T0 on the left and 2P0,2T0 on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal

View SolutionAn insulting container of volume 2V0 is divided in two equal parts by a diathermic (conducting) fixed piston. The left part contains one mole of monoatomic ideal gas whereas right part contains two moles of the same gas. Initial pressue on each side is P0. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) initial temperature in the two sides, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionAn adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficient time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionA cylindrical vessel made of thermally insulating material is divided into two equal parts by an insulating and. Movable piston. Both parts contain ideal monoatomic gas . The gas in the left part is supplied heat such that the volume of right part becomes one-eight of its initial volume . Work done by the gas in the right part is
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionShows a cylindrical tube with adiabatic walls and fittled with a diathermic separetor. The separetor can be slid in the tube by and external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separetor remaons in equilibrium at the middle. It is now slid to pisition where it devides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.

View SolutionA cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless position. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be

View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View Solution
